2018年3月22日木曜日
2018年3月15日木曜日
阪大2018問題1:テイラー展開の2次までが一致する多項式、超越関数、代数関数の大小関係
この問題は、とにかくf(x)-g(x)という関数を微分して単調増加であることを示し、f(x)>g(x)が常に成り立つことを丁寧に示せば解ける。
ここでは、この問題においてどうしてこのような不等式が成立しているのか考えて見たい。まずは、テイラー展開を適用してみよう。一般の関数(ただし無限回微分できる性質をもつもの)f(x)のテイラー展開は、次の公式により与えられる。
\[\begin{equation}
f(x+h) = f(x) + \frac{df(x)}{dx} h + \frac{1}{2!}\frac{d^2f(x)}{dx^2} h^2 + \cdots
=\sum_{n=0}^\infty\frac{1}{n!}\frac{d^nf(x)}{dx^n}h^n
\end{equation}\]
この公式をもちいて\(log(1+x)\)などの関数をテイラー展開してみると
\[\begin{equation}
\log(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots
\end{equation}\]
\[\begin{equation}
\frac{x}{\sqrt{1+x}} = x(1+x)^{-1/2} = x\left(1-\frac{x}{2} + \frac{3}{8}x^2 - \frac{5}{16}x^3+\cdots\right)
\end{equation}\]
となる。したがって、与えられた不等式は
\[\begin{equation}
x - \frac{x^2}{2} < x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots <
x-\frac{x^2}{2} + \frac{3}{8}x^3 - \frac{5}{16}x^4+\cdots
\end{equation}\]
である。第二項目までは、どの関数も共通であり、これらの関数の性質に違いが見られるのが3次以降の項の影響であることは明らかである。0<x<1の場合とx>1の場合にわけて、次数ごとに項別に比較をしてもよいかもしれない。ここを出発点にして、いろいろと面白いことが導けるだろう。
ちなみに、不等式の一番左は有限項からなるので「多項式」、真ん中の対数関数は無限べき級数(テイラー展開)となるので「超越関数」、一番右は無限級数にはなるが代数方程式の根として定義できるので「代数関数」である。したがって、この問題は「これら3種類の解析性をもつ関数のうち、最初の2項が一致するものの大小を比較して見た」という問題になっているのである。
ここでは、この問題においてどうしてこのような不等式が成立しているのか考えて見たい。まずは、テイラー展開を適用してみよう。一般の関数(ただし無限回微分できる性質をもつもの)f(x)のテイラー展開は、次の公式により与えられる。
\[\begin{equation}
f(x+h) = f(x) + \frac{df(x)}{dx} h + \frac{1}{2!}\frac{d^2f(x)}{dx^2} h^2 + \cdots
=\sum_{n=0}^\infty\frac{1}{n!}\frac{d^nf(x)}{dx^n}h^n
\end{equation}\]
この公式をもちいて\(log(1+x)\)などの関数をテイラー展開してみると
\[\begin{equation}
\log(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots
\end{equation}\]
\[\begin{equation}
\frac{x}{\sqrt{1+x}} = x(1+x)^{-1/2} = x\left(1-\frac{x}{2} + \frac{3}{8}x^2 - \frac{5}{16}x^3+\cdots\right)
\end{equation}\]
となる。したがって、与えられた不等式は
\[\begin{equation}
x - \frac{x^2}{2} < x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots <
x-\frac{x^2}{2} + \frac{3}{8}x^3 - \frac{5}{16}x^4+\cdots
\end{equation}\]
である。第二項目までは、どの関数も共通であり、これらの関数の性質に違いが見られるのが3次以降の項の影響であることは明らかである。0<x<1の場合とx>1の場合にわけて、次数ごとに項別に比較をしてもよいかもしれない。ここを出発点にして、いろいろと面白いことが導けるだろう。
ちなみに、不等式の一番左は有限項からなるので「多項式」、真ん中の対数関数は無限べき級数(テイラー展開)となるので「超越関数」、一番右は無限級数にはなるが代数方程式の根として定義できるので「代数関数」である。したがって、この問題は「これら3種類の解析性をもつ関数のうち、最初の2項が一致するものの大小を比較して見た」という問題になっているのである。
2018年3月14日水曜日
阪大2018問4の後半:平面と平面の交線を利用する
3次元ビデオゲームや、映画やコマーシャルのCG、プロジェクションマッピングなど、3次元ベクトルデータを回転させたり、拡大縮小したりする処理は重要性を増している。阪大の問4では、こういった実践問題の練習が可能であり、その点からみれば興味深い問題である。しかし、このような計算を手計算で行うのは大変であり、試験問題を(時間内に)解く、という観点から非常に厳しいやり方かもしれない。
理論物理学の観点からすれば、3次元の力学モデルを構築し、1次変換を駆使して自由自在に処理したい、というのは自然な欲求であり、興味深い。このような計算で研鑽を積んでおけばプログラマーになったときにきっと役に立つはずだ。
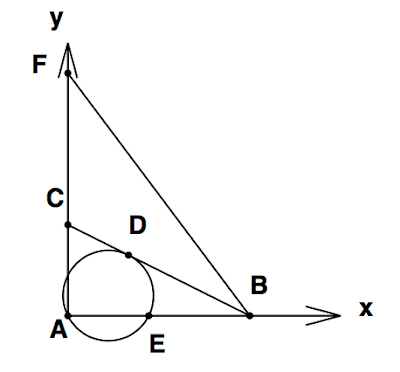
4点PQRSがつくる平面、これは(1)で考えた平面であるが、これが八面体ABCDEFを切り取る断面積を計算する問題である。まずはこの平面の方程式を考えてみよう。平面の方程式の一般形は\(ax+by+cz+d=0\)と表される。したがって、条件が4つあれば未定係数\(a,b,c,d\)が決定できるように思える。しかしそうは問屋が卸さない。なぜだろうか?仮に、4つの異なる点がこの平面にあることがわかったとしよう。方程式は\[ax_i+by_i+cz_i+d=0, \quad (i=1,2,3,4)\]となる。条件を満たす\(i\)番目の点を\((x_i,y_i,z_i)\)と表す。4つの連立方程式をa,b,c,dについて解くことになるが、行列を用いると\[\left(\begin{array}{cccc}x_1 & y_1 & z_1 & 1\\ x_2 & y_2 & z_2 & 1\\ x_3 & y_3 & z_3 & 1\\ x_4 & y_4 & z_4 & 1\end{array}\right) \left(\begin{array}{c}a \\ b\\ c\\ d\end{array}\right) = \vec{0} \]と表せるが、逆行列が存在しても(a,b,c,d)は自明な解、つまりすべて0、になってしまうし、逆行列が存在しなくてもこの連立方程式は解けないことになる。何れにしても手詰まりということである。
これはどうしてかというと、平面の方程式がどのように得られたか考え、この問題の(1)を思い出せばすぐにわかる。平面の方程式は、平面にある一点\((x_0,y_0,z_0)\)と、平面の法線ベクトル\((a,b,c)\)、さらに平面内の任意の点\((x,y,z)\)を使って\[a(x-x_0)+b(y-y_0)+c(z-z_0)=0\]すなわち平面上の直線と法線は直交する(内積が0)という条件により記述される。点\((x,y,z)\)と\((x_0,y_0,z_0)\)を結ぶ直線の上に無い点\((x_,y_1,z_1)\)を用いてもう一つの条件\[a(x-x_1)+b(y-y_1)+c(z-z_1)=0\]までは独立した条件として認めることができる。すなわち、平面上の2点が分かれば(a,b,c,d)のうち2つまでは決めることができる。しかし、3つ目の点\((x_2,y_2,z_2)\)がわかっても、それは役に立たない。というのは、平面内のベクトル\((x-x_2,y-y_2,z-z_2)\)は、先の2つのベクトルとは独立ではなくて、むしろ先の2つのベクトルの線型結合で書けてしまうからである。つまり、\[\left(\begin{array}{c}x-x_2\\y-y_2\\z-z_2\end{array}\right)=p\left(\begin{array}{c}x-x_0\\y-y_0\\z-z_0\end{array}\right) + q\left(\begin{array}{c}x-x_1\\y-y_1\\z-z_1\end{array}\right)\]が成立するので、新しい方程式にならないのだ。ここで\(p,q\)は適当な実数である。平面上のベクトルの一次独立性とは、問(1)の答えに他ならない。
したがって、平面の方程式を決めるなら、平面上の一点を探すこと、そして次は法線ベクトルを直接見つけることなのである。ただし、法線ベクトルは平面上にある3点を見つけることができれば、計算することができる。
法線ベクトルは、平面上の任意のベクトルと直交するので、平面上の2つの独立なベクトルの「外積」を計算するばよいのである。例えば、平面上の3点(三角形をなすような3点)を用いて2つの独立のベクトル\(\mathbf{e}_1=(x_1-x_0, y_1-y_0,z_1-z_0),\quad \mathbf{e}_2=(x_2-x_0, y_2-y_0,z_2-z_0)\)を作り、この2つの外積\(\mathbf{e}_1\times\mathbf{e}_2\)を計算すると、\[\mathbf{e}_1\times\mathbf{e}_2 \parallel \left(\begin{array}{c}a\\ b\\ c\end{array}\right)\]となっているのである。
すなわち、平面の方程式は
\[\begin{equation}\left(\mathbf{e}_1\times\mathbf{e}_2\right)\cdot\left(\mathbf{r}-\mathbf{r}_0\right)={0}\end{equation}\]とまとめることができる。ただし、\(\mathbf{r}=(x,y,z), \quad \mathbf{r}_0=(x_0,y_0,z_0)\)である。
式(1)を使って、まずは平面PQRSの方程式を求めてみよう。 題意に与えられているように、点PはABを\(1-s:s\)に分割する点だから\(\vec{OP}=s\vec{OA}+(1-s)\vec{OB}\)である。これをデカルト座標で表現すると\(P=(1-s,0,s)\)である。同様の計算により\(Q=(0,1-s,s), R=(-1+t,0,-t)\)となる。一次独立なベクトルとして、\(\vec{PQ}\)と\(\vec{PR}\)を取ろう。この2つのベクトルは\[\vec{PQ}=(1-s)\left(\begin{array}{c}-1\\ 1 \\ 0\end{array}\right), \quad \vec{PR}=\left(\begin{array}{c}-2+t+s\\ 0\\ -(t+s)\end{array}\right)\]と計算される。この2つのベクトルの外積\(\vec{PQ}\times\vec{PR}\)は\[\vec{PQ}\times\vec{PR}=\left(\begin{array}{c} -t-s\\ -t-s \\ 2-t-s\end{array}\right)\]となる。点P(1-s,0,s)を使って平面の方程式を書き下すと\[\begin{equation}
(t+s)(x+y)+(t+s-2)z+s-t=0
\end{equation}\]
となる。
次に三角形ABCが作る平面の方程式を求めてみる。この平面上の独立な基底として\(\vec{AB}\)と\(\vec{AC}\)を選ぶ。\[\vec{AB}=\left(\begin{array}{c}1\\ 0\\ -1\end{array}\right), \quad \vec{AC}=\left(\begin{array}{c}0\\ 1\\ -1\end{array}\right)\]であるから、\[\vec{AB}\times\vec{AC} = \left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\]となる。したがって、対応する平面の方程式は\[\begin{equation}{\rm ABC:} \quad x+y+z-1=0\end{equation}\]である。
式(2)から式(3)を引くと\(z=s\), 足すと\(x+y+s-1=0\)を得る。つまり、これが平面PQRSと平面ABCの交線の方程式である。 この交線のうち、交線上にある点Pから点Qまでの線分が求める八面体ABCDEFと平面PQRSの交線である。
平面ABCの隣の面は三角形ABEである。同じように計算すると、
\[
\vec{AE}=\left(\begin{array}{c}0\\ -1\\ -1\end{array}\right), \quad
\vec{AE}\times\vec{AB} = \left(\begin{array}{c}1\\ -1\\ 1\end{array}\right)
\]したがって、点Aを通ることも使うと、平面の方程式は\[\begin{equation}x-y+z-1=0\end{equation}\]となる。これをPQRSの方程式と連立させると、交線の方程式が得られ、それは\[x+(t+s-1)y+s-1=0, \quad (t+s)y-z+s=0\]となる。この線分のうち、Pから始まりxy平面と交わるところまでが求める断面の辺に相当する。交点をTと名付ければ、Tの座標は(上の方程式から)\[T(\frac{t}{t+s},-\frac{s}{t+s},0)\]であることが計算できる。
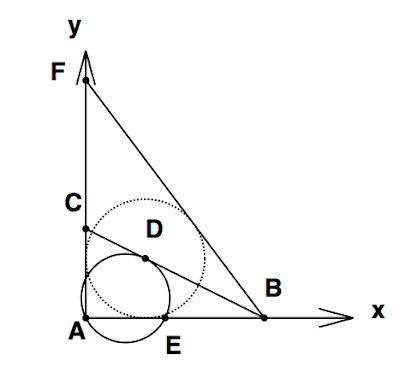
この「地道な作業」を平面BEF, ACD, EDF,CDF、そしておまけとして平面BCDEについて行えば、断面積の形や寸法がわかるだろう。以下、必要な計算の結果だけをまとめて書いておこう。
(1)△BEF:
\[\begin{equation}
\vec{FB}=\left(\begin{array}{c} 1\\ 0 \\ 1\end{array}\right), \quad
\vec{FE}=\left(\begin{array}{c} 0\\ -1 \\ 1\end{array}\right), \quad
\vec{FB}\times\vec{FE} = \left(\begin{array}{c}1\\ -1\\ -1\end{array}\right), \\
x-y-z-1=0
\end{equation}\]
PQRSとの交線は\[y=(1-t-s)x+t-1, \quad z=(t+s)x-t\]
交点はTと\(S(0, -1+t,-t)\)になる。
(2)△EDF:
\[\begin{equation}
\vec{FD}=\left(\begin{array}{c} -1\\ 0 \\ 1\end{array}\right), \quad
\vec{FD}\times\vec{FE} = \left(\begin{array}{c}1\\ 1\\ 1\end{array}\right), \\
x+y+z+1=0
\end{equation}\]
PQRSとの交線は\[x+y-t+1=0, \quad z=-t\]
交点は\(R(-1+t,0,-t)\),S。
(3)△CDF:
\[\begin{equation}
\vec{FC}=\left(\begin{array}{c} 0\\ 1 \\ 1\end{array}\right), \quad
\vec{FC}\times\vec{FD} = \left(\begin{array}{c}1\\ -1\\ 1\end{array}\right), \\
x-y-z+1=0
\end{equation}\]
PQRSとの交線は\[x+(t+s-1)y-t+1=0, \quad z=(t+s)y-t\]
交点はR,\[U(-\frac{s}{t+s},\frac{t}{t+s},0)\]
(4)△ACD
\[\begin{equation}
\vec{AD}=\left(\begin{array}{c} -1\\ 0 \\ -1\end{array}\right), \quad
\vec{AD}\times\vec{AC} = \left(\begin{array}{c}1\\ -1\\ -1\end{array}\right), \\
x-y-z+1=0
\end{equation}\]
PQRSとの交線は\[(t+s-1)x+y+s-1=0, \quad z=(t+s)x+s\]
交点はU,Q。
以上より、断面は六角形QPTSRUであり、直線PQ, TU, SRはxy平面に対し水平であるから、互いに平行の関係にある。したがって、六角形の面積は2つの台形QPTUとRSTUに分解して求めることができる。PQ=\(\sqrt{2}(1-s)\), SR=\(\sqrt{2}(1-t)\), TU=\(\sqrt{2}\)であることはすぐにわかる。また、PQとTUの距離はs、TUとSRの距離はtであることも(座標の情報より)自明である。したがって、六角形の面積Xは
\[
X=\frac{s(2-s)}{\sqrt{2}} + \frac{t(2-t)}{\sqrt{2}} = \sqrt{2}(t+s) - \frac{1}{\sqrt{2}}(t^2+s^2)
\]
とかける。\(t^2+s^2 = (t+s)^2 - 2ts\)であることを用い、さらに\(t+s=2/3\)という条件を代入するとXはsの二次式になる。
\[
X= \frac{5\sqrt{2}}{9}-\sqrt{2}\left(s-\frac{1}{3}\right)^2
\]
したがって、最大値は\(s=t=1/3\)のときで\(5\sqrt{2}/{9}\)である。
\(s+t=2/3\)という条件は最後の最後まで使わない方がよい。なぜか途中で中途半端に使用すると、まちがった答えへといってしまう(非常に不思議)。
この問題では、3次元空間中の座標を使って解いたが、回転によってもう少し見通しをよくしてから解くこともできる。次はその方法を試してみよう。
理論物理学の観点からすれば、3次元の力学モデルを構築し、1次変換を駆使して自由自在に処理したい、というのは自然な欲求であり、興味深い。このような計算で研鑽を積んでおけばプログラマーになったときにきっと役に立つはずだ。
4点PQRSがつくる平面、これは(1)で考えた平面であるが、これが八面体ABCDEFを切り取る断面積を計算する問題である。まずはこの平面の方程式を考えてみよう。平面の方程式の一般形は\(ax+by+cz+d=0\)と表される。したがって、条件が4つあれば未定係数\(a,b,c,d\)が決定できるように思える。しかしそうは問屋が卸さない。なぜだろうか?仮に、4つの異なる点がこの平面にあることがわかったとしよう。方程式は\[ax_i+by_i+cz_i+d=0, \quad (i=1,2,3,4)\]となる。条件を満たす\(i\)番目の点を\((x_i,y_i,z_i)\)と表す。4つの連立方程式をa,b,c,dについて解くことになるが、行列を用いると\[\left(\begin{array}{cccc}x_1 & y_1 & z_1 & 1\\ x_2 & y_2 & z_2 & 1\\ x_3 & y_3 & z_3 & 1\\ x_4 & y_4 & z_4 & 1\end{array}\right) \left(\begin{array}{c}a \\ b\\ c\\ d\end{array}\right) = \vec{0} \]と表せるが、逆行列が存在しても(a,b,c,d)は自明な解、つまりすべて0、になってしまうし、逆行列が存在しなくてもこの連立方程式は解けないことになる。何れにしても手詰まりということである。
これはどうしてかというと、平面の方程式がどのように得られたか考え、この問題の(1)を思い出せばすぐにわかる。平面の方程式は、平面にある一点\((x_0,y_0,z_0)\)と、平面の法線ベクトル\((a,b,c)\)、さらに平面内の任意の点\((x,y,z)\)を使って\[a(x-x_0)+b(y-y_0)+c(z-z_0)=0\]すなわち平面上の直線と法線は直交する(内積が0)という条件により記述される。点\((x,y,z)\)と\((x_0,y_0,z_0)\)を結ぶ直線の上に無い点\((x_,y_1,z_1)\)を用いてもう一つの条件\[a(x-x_1)+b(y-y_1)+c(z-z_1)=0\]までは独立した条件として認めることができる。すなわち、平面上の2点が分かれば(a,b,c,d)のうち2つまでは決めることができる。しかし、3つ目の点\((x_2,y_2,z_2)\)がわかっても、それは役に立たない。というのは、平面内のベクトル\((x-x_2,y-y_2,z-z_2)\)は、先の2つのベクトルとは独立ではなくて、むしろ先の2つのベクトルの線型結合で書けてしまうからである。つまり、\[\left(\begin{array}{c}x-x_2\\y-y_2\\z-z_2\end{array}\right)=p\left(\begin{array}{c}x-x_0\\y-y_0\\z-z_0\end{array}\right) + q\left(\begin{array}{c}x-x_1\\y-y_1\\z-z_1\end{array}\right)\]が成立するので、新しい方程式にならないのだ。ここで\(p,q\)は適当な実数である。平面上のベクトルの一次独立性とは、問(1)の答えに他ならない。
したがって、平面の方程式を決めるなら、平面上の一点を探すこと、そして次は法線ベクトルを直接見つけることなのである。ただし、法線ベクトルは平面上にある3点を見つけることができれば、計算することができる。
法線ベクトルは、平面上の任意のベクトルと直交するので、平面上の2つの独立なベクトルの「外積」を計算するばよいのである。例えば、平面上の3点(三角形をなすような3点)を用いて2つの独立のベクトル\(\mathbf{e}_1=(x_1-x_0, y_1-y_0,z_1-z_0),\quad \mathbf{e}_2=(x_2-x_0, y_2-y_0,z_2-z_0)\)を作り、この2つの外積\(\mathbf{e}_1\times\mathbf{e}_2\)を計算すると、\[\mathbf{e}_1\times\mathbf{e}_2 \parallel \left(\begin{array}{c}a\\ b\\ c\end{array}\right)\]となっているのである。
すなわち、平面の方程式は
\[\begin{equation}\left(\mathbf{e}_1\times\mathbf{e}_2\right)\cdot\left(\mathbf{r}-\mathbf{r}_0\right)={0}\end{equation}\]とまとめることができる。ただし、\(\mathbf{r}=(x,y,z), \quad \mathbf{r}_0=(x_0,y_0,z_0)\)である。
式(1)を使って、まずは平面PQRSの方程式を求めてみよう。 題意に与えられているように、点PはABを\(1-s:s\)に分割する点だから\(\vec{OP}=s\vec{OA}+(1-s)\vec{OB}\)である。これをデカルト座標で表現すると\(P=(1-s,0,s)\)である。同様の計算により\(Q=(0,1-s,s), R=(-1+t,0,-t)\)となる。一次独立なベクトルとして、\(\vec{PQ}\)と\(\vec{PR}\)を取ろう。この2つのベクトルは\[\vec{PQ}=(1-s)\left(\begin{array}{c}-1\\ 1 \\ 0\end{array}\right), \quad \vec{PR}=\left(\begin{array}{c}-2+t+s\\ 0\\ -(t+s)\end{array}\right)\]と計算される。この2つのベクトルの外積\(\vec{PQ}\times\vec{PR}\)は\[\vec{PQ}\times\vec{PR}=\left(\begin{array}{c} -t-s\\ -t-s \\ 2-t-s\end{array}\right)\]となる。点P(1-s,0,s)を使って平面の方程式を書き下すと\[\begin{equation}
(t+s)(x+y)+(t+s-2)z+s-t=0
\end{equation}\]
となる。
次に三角形ABCが作る平面の方程式を求めてみる。この平面上の独立な基底として\(\vec{AB}\)と\(\vec{AC}\)を選ぶ。\[\vec{AB}=\left(\begin{array}{c}1\\ 0\\ -1\end{array}\right), \quad \vec{AC}=\left(\begin{array}{c}0\\ 1\\ -1\end{array}\right)\]であるから、\[\vec{AB}\times\vec{AC} = \left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\]となる。したがって、対応する平面の方程式は\[\begin{equation}{\rm ABC:} \quad x+y+z-1=0\end{equation}\]である。
式(2)から式(3)を引くと\(z=s\), 足すと\(x+y+s-1=0\)を得る。つまり、これが平面PQRSと平面ABCの交線の方程式である。 この交線のうち、交線上にある点Pから点Qまでの線分が求める八面体ABCDEFと平面PQRSの交線である。
平面ABCの隣の面は三角形ABEである。同じように計算すると、
\[
\vec{AE}=\left(\begin{array}{c}0\\ -1\\ -1\end{array}\right), \quad
\vec{AE}\times\vec{AB} = \left(\begin{array}{c}1\\ -1\\ 1\end{array}\right)
\]したがって、点Aを通ることも使うと、平面の方程式は\[\begin{equation}x-y+z-1=0\end{equation}\]となる。これをPQRSの方程式と連立させると、交線の方程式が得られ、それは\[x+(t+s-1)y+s-1=0, \quad (t+s)y-z+s=0\]となる。この線分のうち、Pから始まりxy平面と交わるところまでが求める断面の辺に相当する。交点をTと名付ければ、Tの座標は(上の方程式から)\[T(\frac{t}{t+s},-\frac{s}{t+s},0)\]であることが計算できる。
この「地道な作業」を平面BEF, ACD, EDF,CDF、そしておまけとして平面BCDEについて行えば、断面積の形や寸法がわかるだろう。以下、必要な計算の結果だけをまとめて書いておこう。
(1)△BEF:
\[\begin{equation}
\vec{FB}=\left(\begin{array}{c} 1\\ 0 \\ 1\end{array}\right), \quad
\vec{FE}=\left(\begin{array}{c} 0\\ -1 \\ 1\end{array}\right), \quad
\vec{FB}\times\vec{FE} = \left(\begin{array}{c}1\\ -1\\ -1\end{array}\right), \\
x-y-z-1=0
\end{equation}\]
PQRSとの交線は\[y=(1-t-s)x+t-1, \quad z=(t+s)x-t\]
交点はTと\(S(0, -1+t,-t)\)になる。
(2)△EDF:
\[\begin{equation}
\vec{FD}=\left(\begin{array}{c} -1\\ 0 \\ 1\end{array}\right), \quad
\vec{FD}\times\vec{FE} = \left(\begin{array}{c}1\\ 1\\ 1\end{array}\right), \\
x+y+z+1=0
\end{equation}\]
PQRSとの交線は\[x+y-t+1=0, \quad z=-t\]
交点は\(R(-1+t,0,-t)\),S。
(3)△CDF:
\[\begin{equation}
\vec{FC}=\left(\begin{array}{c} 0\\ 1 \\ 1\end{array}\right), \quad
\vec{FC}\times\vec{FD} = \left(\begin{array}{c}1\\ -1\\ 1\end{array}\right), \\
x-y-z+1=0
\end{equation}\]
PQRSとの交線は\[x+(t+s-1)y-t+1=0, \quad z=(t+s)y-t\]
交点はR,\[U(-\frac{s}{t+s},\frac{t}{t+s},0)\]
(4)△ACD
\[\begin{equation}
\vec{AD}=\left(\begin{array}{c} -1\\ 0 \\ -1\end{array}\right), \quad
\vec{AD}\times\vec{AC} = \left(\begin{array}{c}1\\ -1\\ -1\end{array}\right), \\
x-y-z+1=0
\end{equation}\]
PQRSとの交線は\[(t+s-1)x+y+s-1=0, \quad z=(t+s)x+s\]
交点はU,Q。
以上より、断面は六角形QPTSRUであり、直線PQ, TU, SRはxy平面に対し水平であるから、互いに平行の関係にある。したがって、六角形の面積は2つの台形QPTUとRSTUに分解して求めることができる。PQ=\(\sqrt{2}(1-s)\), SR=\(\sqrt{2}(1-t)\), TU=\(\sqrt{2}\)であることはすぐにわかる。また、PQとTUの距離はs、TUとSRの距離はtであることも(座標の情報より)自明である。したがって、六角形の面積Xは
\[
X=\frac{s(2-s)}{\sqrt{2}} + \frac{t(2-t)}{\sqrt{2}} = \sqrt{2}(t+s) - \frac{1}{\sqrt{2}}(t^2+s^2)
\]
とかける。\(t^2+s^2 = (t+s)^2 - 2ts\)であることを用い、さらに\(t+s=2/3\)という条件を代入するとXはsの二次式になる。
\[
X= \frac{5\sqrt{2}}{9}-\sqrt{2}\left(s-\frac{1}{3}\right)^2
\]
したがって、最大値は\(s=t=1/3\)のときで\(5\sqrt{2}/{9}\)である。
\(s+t=2/3\)という条件は最後の最後まで使わない方がよい。なぜか途中で中途半端に使用すると、まちがった答えへといってしまう(非常に不思議)。
この問題では、3次元空間中の座標を使って解いたが、回転によってもう少し見通しをよくしてから解くこともできる。次はその方法を試してみよう。
2018年3月8日木曜日
阪大2018問題4の前半:線形代数(ベクトル空間)に関する良い問題
阪大数学(2018)のの問題4は、空間図形の問題であるが、東大の問題6や問題3と違って、線形代数やベクトル空間の考え方が利用できる素晴らしい問題である。このような良い問題を解いて阪大に進んだ学生たちは、あの変な「ベクトル問題」を解いて東大に進んだ場合よりも、大学に入ってからの進歩がきっと速いだろう。
(1)と(2)は簡単に解けるのでさっそく取り掛かってみよう。注意:「簡単に解けるから重要ではない」というのは間違いである。簡単に解けるが数学の本質を捉えた重要な問題もある。それがこの問題である。
まず、(数学上の)3次元ベクトル空間を、(物理的な)実際の3次元空間と一致させることができるのは自明としよう。3次元ベクトル空間に属する任意のベクトルは、一次独立な3つのベクトル(基底という)の線型結合で表すことができる。線型独立の正確な定義は大学の線形代数で習うのでここでは飛ばすが、高校生の段階では「互いに直交する3つのベクトル」程度の理解から始めればよいと思う。(そのうち、直交する必要がないことは自然と理解できるであろう。)
2次元空間、すなわち平面においては、次元が1つ下がるので、一次独立なベクトルの数、すなわち基底の数は2つに減る。一次独立を理解する最初の一歩は、「直交する2つのベクトル」になるわけだが、2次元空間なら「非直交な基底」のイメージがしやすいだろうから、ここで簡単に述べておく。そもそも、(1)を解くにも非直交な基底の理解は必要になる。それは、平行でない2つのベクトルの組みのことである。例えば、\(\vec{PQ}\)と\(\vec{PR}\)は一次独立である。デカルト座標系で計算してみるとすぐにわかると思うが、この2つのベクトルは平行でないからである。
3点P,Q,Rが決まると、P、Q、Rを通過する平面が決まる。この平面の基準点(つまり原点に相当するもの)としてPを選ぼう。「この平面内にある任意の点Xに対応するベクトル \(\vec{PX}\)は、この平面に相当する2次元ベクトル空間の基底2つの線型結合で表せる」というのが、線形代数の重要な定理の1つである。上で見たように、この基底として\(\vec{PQ}\)と\(\vec{PR}\)を選ぶことができる。したがって、\[\begin{equation}\vec{PX}=x\vec{PQ}+y\vec{PR}\end{equation}\]と表せる。\(x,y\)は実数であり、この平面における「座標(x,y)」に相当するものである。基底が非直交なので、この座標系は非直交座標である(相対性理論で出てくるような座標である)。
(1)で聞かれているのは、「X=S」とできるかどうか?ということである。できるならばSは平面PQRにあることになる。できなければ、平面PQRにはないということになる。与えられた3次元デカルト座標の値を 代入して、丁寧に計算していくと
\[ x=-\frac{t-1}{s-1}, \quad y=1\]となり、Sは平面PQR上にあることが示せる。
(2)はもっと簡単で、\[\vec{LM}=\left(\begin{array}{c}\frac{t+s-2}{2}\\ \frac{t+s-2}{2}\\ -(t+s)\end{array}\right)\]と表せることを利用して、ピタゴラスの定理を用いて長さ(の2乗)を\(q=t+s\)の2次関数として表わし、その最小値ががqの定義域の中においてどこで起きるか調べるだけでよい。\(m^2 = 4/3, q=t+s=2/3\)の時が答えに相当する状況である。
(1)と(2)は簡単に解けるのでさっそく取り掛かってみよう。注意:「簡単に解けるから重要ではない」というのは間違いである。簡単に解けるが数学の本質を捉えた重要な問題もある。それがこの問題である。
座標空間に6点A(0,0,1), B(1.0,0), C(0,1,0), D(-1,0,0), E(0,-1,0), F(0,0,-1)を頂点とする正八面体ABCDEFがある。\(s, t\)を\(0<s<1, 0<t<1\)を満たす実数とする。P,QはAB, ACを\(1-s:s\)にそれぞれ内分する点とし、R,SはFD, FEをそれぞれ\(1-t:t\)に内分する点とする。
(1)4つの点P,Q,R,S が同一平面上にあることを示せ。(1)が特に重要である。ベクトル空間の線型独立や線型従属を理解しているかどうかを問う問題であり、これがきちんと書ければ(予備校や高校の教科書が提供するような解答法ではない)、大学の線形代数の最初の関門はすでに乗り越えたと思ってよいだろう。
(2)PQの中点をL、RSの中点をMとする。\(s,t\)が問題で与えられた範囲を動くとき、線分LMの最小値mを求めよ。
まず、(数学上の)3次元ベクトル空間を、(物理的な)実際の3次元空間と一致させることができるのは自明としよう。3次元ベクトル空間に属する任意のベクトルは、一次独立な3つのベクトル(基底という)の線型結合で表すことができる。線型独立の正確な定義は大学の線形代数で習うのでここでは飛ばすが、高校生の段階では「互いに直交する3つのベクトル」程度の理解から始めればよいと思う。(そのうち、直交する必要がないことは自然と理解できるであろう。)
2次元空間、すなわち平面においては、次元が1つ下がるので、一次独立なベクトルの数、すなわち基底の数は2つに減る。一次独立を理解する最初の一歩は、「直交する2つのベクトル」になるわけだが、2次元空間なら「非直交な基底」のイメージがしやすいだろうから、ここで簡単に述べておく。そもそも、(1)を解くにも非直交な基底の理解は必要になる。それは、平行でない2つのベクトルの組みのことである。例えば、\(\vec{PQ}\)と\(\vec{PR}\)は一次独立である。デカルト座標系で計算してみるとすぐにわかると思うが、この2つのベクトルは平行でないからである。
3点P,Q,Rが決まると、P、Q、Rを通過する平面が決まる。この平面の基準点(つまり原点に相当するもの)としてPを選ぼう。「この平面内にある任意の点Xに対応するベクトル \(\vec{PX}\)は、この平面に相当する2次元ベクトル空間の基底2つの線型結合で表せる」というのが、線形代数の重要な定理の1つである。上で見たように、この基底として\(\vec{PQ}\)と\(\vec{PR}\)を選ぶことができる。したがって、\[\begin{equation}\vec{PX}=x\vec{PQ}+y\vec{PR}\end{equation}\]と表せる。\(x,y\)は実数であり、この平面における「座標(x,y)」に相当するものである。基底が非直交なので、この座標系は非直交座標である(相対性理論で出てくるような座標である)。
(1)で聞かれているのは、「X=S」とできるかどうか?ということである。できるならばSは平面PQRにあることになる。できなければ、平面PQRにはないということになる。与えられた3次元デカルト座標の値を 代入して、丁寧に計算していくと
\[ x=-\frac{t-1}{s-1}, \quad y=1\]となり、Sは平面PQR上にあることが示せる。
(2)はもっと簡単で、\[\vec{LM}=\left(\begin{array}{c}\frac{t+s-2}{2}\\ \frac{t+s-2}{2}\\ -(t+s)\end{array}\right)\]と表せることを利用して、ピタゴラスの定理を用いて長さ(の2乗)を\(q=t+s\)の2次関数として表わし、その最小値ががqの定義域の中においてどこで起きるか調べるだけでよい。\(m^2 = 4/3, q=t+s=2/3\)の時が答えに相当する状況である。
三角関数のベキ乗をフーリエ級数展開する
阪大2018問題3を解いているうちに、三角関数のベキ乗、例えば\(\cos^n x\)などをフーリエ級数で展開することを思いついた。積分するときは、三角関数のベキ乗を直接計算することはできず、必ず\(\cos nx\)とか\(\sin nx\)のような形に変換してから積分計算しなくてはならない。これはつまり、フーリエ級数展開するということと同じではないか?
三角関数のn乗が一般にどのように展開されるのかわからないので、まずはいくつか具体例を計算してみよう。
(1) n=2
\[\begin{equation}\cos^2 x = \frac{1}{2} + \frac{1}{2}\cos 2x , \quad \sin^2 x = \frac{1}{2} - \frac{1}{2}\cos 2x\end{equation}\]
(2) n=3
\[ \begin{equation} \cos^3 x = \frac{3}{4}\cos x + \frac{1}{4}\cos 3x, \quad
\sin^3 x = \frac{3}{4}\sin x - \frac{1}{4}\sin 3x\end{equation}\]
(3) n=4
\[\begin{equation} \cos^4 x = \frac{3}{8} + \frac{1}{2}\cos 2x + \frac{1}{8}\cos 4x, \quad \sin^4 x = \frac{3}{8} - \frac{1}{2}\cos 2x + \frac{1}{8}\cos 4x\end{equation}\]
(4) n=5
\[\begin{equation}\cos^5 x = \frac{5}{8}\cos x + \frac{5}{16} \cos 3x + \frac{1}{16}\cos 5x, \quad \sin^5 x = \frac{5}{8}\sin x - \frac{5}{16}\sin 3x + \frac{1}{16}\sin 5x\end{equation}\]
この結果を得るための計算手法について少しだけ言及しておこう。(1)n=2の場合は高校の数学でもやるのでおなじみだろう。いわゆる倍角公式とか、加法定理とかいうものである。(3)n=4の場合は、n=2の公式を応用して得ることができる。これは前回の議論で考察した。 骨が折れるのが(2)や(4)に相当するn=奇数の場合だが、これも加法定理を応用し、n=2の場合と組み合わせれば、高校数学の範囲で計算することができる。例えば、\(\sin^3 x=\sin^2 x \cdot \sin x\)と分解し、2乗の部分にn=2の公式を適用する。
\[\begin{equation} \frac{1-\cos 2x}{2} \cdot \sin x = \frac{1}{2}\sin x - \frac{1}{2}\cos 2x \sin x\end{equation}\]となる。右辺第二項を、加法定理の逆
\[\begin{equation}2\cos 2x \sin x = \sin (x + 2x) + \sin (x - 2x)\end{equation}\]を使って書き直すと、
\[\begin{equation} \sin^3 x=\frac{1}{2}\sin x - \frac{1}{4}\left(\sin 3x - \sin x\right) =\frac{3}{4}\sin x - \frac{1}{4}\sin 3x\end{equation}\]を得る。
ここまでの結果をみて、ある程度傾向が見えてきたのではないかと思う。まず、n=偶数の場合、三角関数をべき乗したものの全てが偶関数になる。したがって、そのフーリエ級数(ここでは、三角関数の有限和も「級数」と呼ぶことにしよう)は余弦関数のみの和となている。さらに、含まれる余弦関数の周波数は0, 2, 4, ..., n=偶数のものに限られ(これをパリティが0の周波数と呼ぶことにしよう)、1,3,...といったパリティが1の周波数成分はフーリエ級数展開の中に含まれないという特徴が見られる。また、級数の展開係数の分母は\(2^n\)になっているらしく、各項の分子の総和が\(2^n\)に等しくなっている。つまり、展開係数の和はどんな場合も1になっている。
n=奇数の場合は、余弦の場合は偶関数なので、上と同じように\(\cos kx\)による級数展開となるが、正弦の場合には奇関数となるので、級数展開には\(\sin kx\)のみが使われる。符号も次数に対し交代で入ってくるようだ。
もう一つ面白いのは、n=奇数の場合は、\(\cos x\)や\(\sin x\)の成分(展開係数の大きさのこと)が最大、つまり主成分となる点である。n=1,3,5の場合をまとめて見ると
n =1 n=3 n=5
100% 75% 62.5%
といった具合である。
nが大きいときに、\(\sin^n x \simeq \frac{1}{2}\sin x\)と近似して、たとえば積分しても結構いい値がでるのではないだろうか?数値実験してみるとおもしろいかもしれない。
またn=偶数の時は、1の成分と\(\cos 2x\)の成分がほぼ同じくらいの割合で主成分になっている。すなわち\(\cos ^ nx \simeq \frac{1}{2}\left(1+\cos 2x\right)\)と近似しても結構いい値が出るのではないか?これも調べて見たらおもしろいだろう。
これらの性質を統一的に公式にまとめ上げるには、オイラーの公式\(\cos x + i\sin x={\rm e}^{ix}\)を使うのがよいだろう。例えば、n=3の場合について考えて見る。
\[\begin{equation} \left(\cos x + i\sin x\right)^3 = \left({\rm e}^{ix}\right)^3 ={\rm e}^{3ix} = \cos 3x + i \sin 3x \end{equation}\]であるが、一番左を二項展開すると、\[\begin{equation}\cos^3 x + 3i\cos^2 x \sin x - 3\cos x \sin^2 x - i\sin^3 x = \cos 3x + i \sin 3x\end{equation}\]を得る。実数部と虚数部を整理して書くと、
\[\begin{equation} \left(\cos^3 x -3\cos x \sin^2 x - \cos 3x\right) + i\left( 3\cos^2 x \sin x - \sin^3 x - \sin 3x\right) = 0\end{equation}\]となる。この式の複素共役を作って、(10)式と足したり、引いたりすることで、三角関数の3乗の公式を得ることができる。が、まだシステマティックに計算するには見通しが悪い。この先をどのように進めていくかは、次の課題としよう。一つ確かなのは、係数は二項展開の係数と関連付けられそうだという点である。この点には着目すべきだと思う。
ここまでで思いついたことで、簡単に証明できそうなことをメモしておく。
三角関数のn乗が一般にどのように展開されるのかわからないので、まずはいくつか具体例を計算してみよう。
(1) n=2
\[\begin{equation}\cos^2 x = \frac{1}{2} + \frac{1}{2}\cos 2x , \quad \sin^2 x = \frac{1}{2} - \frac{1}{2}\cos 2x\end{equation}\]
(2) n=3
\[ \begin{equation} \cos^3 x = \frac{3}{4}\cos x + \frac{1}{4}\cos 3x, \quad
\sin^3 x = \frac{3}{4}\sin x - \frac{1}{4}\sin 3x\end{equation}\]
(3) n=4
\[\begin{equation} \cos^4 x = \frac{3}{8} + \frac{1}{2}\cos 2x + \frac{1}{8}\cos 4x, \quad \sin^4 x = \frac{3}{8} - \frac{1}{2}\cos 2x + \frac{1}{8}\cos 4x\end{equation}\]
(4) n=5
\[\begin{equation}\cos^5 x = \frac{5}{8}\cos x + \frac{5}{16} \cos 3x + \frac{1}{16}\cos 5x, \quad \sin^5 x = \frac{5}{8}\sin x - \frac{5}{16}\sin 3x + \frac{1}{16}\sin 5x\end{equation}\]
この結果を得るための計算手法について少しだけ言及しておこう。(1)n=2の場合は高校の数学でもやるのでおなじみだろう。いわゆる倍角公式とか、加法定理とかいうものである。(3)n=4の場合は、n=2の公式を応用して得ることができる。これは前回の議論で考察した。 骨が折れるのが(2)や(4)に相当するn=奇数の場合だが、これも加法定理を応用し、n=2の場合と組み合わせれば、高校数学の範囲で計算することができる。例えば、\(\sin^3 x=\sin^2 x \cdot \sin x\)と分解し、2乗の部分にn=2の公式を適用する。
\[\begin{equation} \frac{1-\cos 2x}{2} \cdot \sin x = \frac{1}{2}\sin x - \frac{1}{2}\cos 2x \sin x\end{equation}\]となる。右辺第二項を、加法定理の逆
\[\begin{equation}2\cos 2x \sin x = \sin (x + 2x) + \sin (x - 2x)\end{equation}\]を使って書き直すと、
\[\begin{equation} \sin^3 x=\frac{1}{2}\sin x - \frac{1}{4}\left(\sin 3x - \sin x\right) =\frac{3}{4}\sin x - \frac{1}{4}\sin 3x\end{equation}\]を得る。
ここまでの結果をみて、ある程度傾向が見えてきたのではないかと思う。まず、n=偶数の場合、三角関数をべき乗したものの全てが偶関数になる。したがって、そのフーリエ級数(ここでは、三角関数の有限和も「級数」と呼ぶことにしよう)は余弦関数のみの和となている。さらに、含まれる余弦関数の周波数は0, 2, 4, ..., n=偶数のものに限られ(これをパリティが0の周波数と呼ぶことにしよう)、1,3,...といったパリティが1の周波数成分はフーリエ級数展開の中に含まれないという特徴が見られる。また、級数の展開係数の分母は\(2^n\)になっているらしく、各項の分子の総和が\(2^n\)に等しくなっている。つまり、展開係数の和はどんな場合も1になっている。
n=奇数の場合は、余弦の場合は偶関数なので、上と同じように\(\cos kx\)による級数展開となるが、正弦の場合には奇関数となるので、級数展開には\(\sin kx\)のみが使われる。符号も次数に対し交代で入ってくるようだ。
もう一つ面白いのは、n=奇数の場合は、\(\cos x\)や\(\sin x\)の成分(展開係数の大きさのこと)が最大、つまり主成分となる点である。n=1,3,5の場合をまとめて見ると
n =1 n=3 n=5
100% 75% 62.5%
といった具合である。
nが大きいときに、\(\sin^n x \simeq \frac{1}{2}\sin x\)と近似して、たとえば積分しても結構いい値がでるのではないだろうか?数値実験してみるとおもしろいかもしれない。
またn=偶数の時は、1の成分と\(\cos 2x\)の成分がほぼ同じくらいの割合で主成分になっている。すなわち\(\cos ^ nx \simeq \frac{1}{2}\left(1+\cos 2x\right)\)と近似しても結構いい値が出るのではないか?これも調べて見たらおもしろいだろう。
これらの性質を統一的に公式にまとめ上げるには、オイラーの公式\(\cos x + i\sin x={\rm e}^{ix}\)を使うのがよいだろう。例えば、n=3の場合について考えて見る。
\[\begin{equation} \left(\cos x + i\sin x\right)^3 = \left({\rm e}^{ix}\right)^3 ={\rm e}^{3ix} = \cos 3x + i \sin 3x \end{equation}\]であるが、一番左を二項展開すると、\[\begin{equation}\cos^3 x + 3i\cos^2 x \sin x - 3\cos x \sin^2 x - i\sin^3 x = \cos 3x + i \sin 3x\end{equation}\]を得る。実数部と虚数部を整理して書くと、
\[\begin{equation} \left(\cos^3 x -3\cos x \sin^2 x - \cos 3x\right) + i\left( 3\cos^2 x \sin x - \sin^3 x - \sin 3x\right) = 0\end{equation}\]となる。この式の複素共役を作って、(10)式と足したり、引いたりすることで、三角関数の3乗の公式を得ることができる。が、まだシステマティックに計算するには見通しが悪い。この先をどのように進めていくかは、次の課題としよう。一つ確かなのは、係数は二項展開の係数と関連付けられそうだという点である。この点には着目すべきだと思う。
ここまでで思いついたことで、簡単に証明できそうなことをメモしておく。
三角関数のn乗のフーリエ級数展開において、\(\cos nx\)や\(\sin nx\)に対応する成分の展開係数は, \(\frac{1}{2^{n-1}}\)になっているように見える。これを帰納法で証明することは可能かどうか?
阪大2018問題3(2):グラフの対称性を利用する
(2)では、グラフの対称性をネタに問題が作られている。
φが0から2π/3まで変化するとき、(x,y)はx軸上の点(-3,0)から、「棘の張り出し」に相当する点\((3/2, 3\sqrt{3}/2)\)まで滑らかに変化する。これをθ(つまりt)の範囲に直すと、-π/2からπ/6までに相当する。tは0からなので、この範囲ではまずい。t=0のとき、φ=π/2であるが、この点に対応するのが(1,2)である。
次は、φが2π/3から4π/3まで変化するときであるが、このときは点\((3/2,3\sqrt{3}/2)\)から、x軸に線対称な点\((3/2,-3\sqrt{3}/2)\)まで滑らかに変化する。この範囲はtでいうとπ/6から5π/6であるが、tはπ/2までであるから\(\frac{\pi}{6} \leqq t \leqq \frac{\pi}{2}\)である。t=π/2というのはφ=πの点で、x軸上の点(1,0)に相当する。
まとめると、\(0\leqq t \leqq \frac{\pi}{6}\)において(これを領域Iと呼ぼう)、Cは点(1,2)から点\((\frac{3}{2},\frac{3\sqrt{3}}{2})\)まで滑らかに変化する単調増加なグラフである。一方、\(\frac{\pi}{6}\leqq t \leqq \frac{\pi}{2}\)では(これを領域IIと呼ぼう)、Cは点\((\frac{3}{2},\frac{3\sqrt{3}}{2})\)から点(1,0)まで滑らかに変化する単調減少のグラフである。2つの領域を同時に考えると、\(1\leqq x \leqq \frac{3\sqrt{3}}{2}\)の領域でy=y(x)は二価関数となる(つまり、y=f(x)を考えた時、同じxに対して異なる2つのyの値が対応しているということで、グラフで考えるとx軸に対する垂線がyのグラフと異なる2箇所で交点をもつということ)。ただし、yやxをtの関数と見なせば、それぞれは一価関数である(同じxでも\(x=f(t_1)=f(t_2)\)となって、異なるtになっているということ)。
領域Iと領域IIをグラフで観察すると、その形から常に\(g(I) > g(II) > 0\)が成立しているのがわかる。 したがって、\(g(I)+g(II) > 0\)は自明であるので、上の関係を用いると\[\left\{g(I)+g(II)\right\}\left\{g(I)-g(II)\right\} > 0\]が成り立つのは自明である。領域Iと領域IIはtの立場からすると、\(t_1\)が属するのが領域I, \(t_2\)が属するのが領域IIであるから、題意は証明されたといってよい。つまり、\(f(t_1)=f(t_2)\)という条件は、Cの「二価性」から, \(t_1\)はIに、\(t_2\)はIIに属し、両者が同じ領域に属することはないことを保証する条件に相当している。この部分が読み取れれば、証明の残りの部分はまさに自明なのである。
ここまでくれば、(3)は簡単、と書こうと思ったが、この問題は実によく練られていて、まだ油断ができない。計算すべきは領域Iにおけるy(t)とx軸の間の面積から、領域IIにおけるy(t)とx軸の間の面積を引いたもの(差)である。したがって、
\[\begin{eqnarray}S &=&\int_1^{\frac{3\sqrt{3}}{2}}ydx - \int_1^{\frac{3\sqrt{3}}{2}}ydx \\ &=&\int_0^{\frac{\pi}{6}}g(t)\frac{dx}{dt}dt - \int^{\frac{\pi}{6}}_{\frac{\pi}{2}}g(t)\frac{dx}{dt}dt \\
&=&\int_0^{\frac{\pi}{6}}g(t)\frac{dx}{dt}dt +\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}g(t)\frac{dx}{dt}dt \\
&=&\int_{0}^{\frac{\pi}{2}}g(t)\frac{dx}{dt}dt \end{eqnarray}\]を計算すればよい。
ここで変数変換のために導入した\(dx = \frac{dx}{dt}dt\) という関係式だが、これはニュートンの微分記号x'に比べて、ライプニッツの微分記号dxの方が強力であることを示す、有名な一例である。ニュートンの記号は、計算における筆記量を削減してくれるので「便利」ではあるが、微分演算が通常の割り算や代数演算に従って変形できる性質を持つことを示してはくれないので発展性の観点からは「不便」なのである。また、ニュートンがy'とかy''という記号を導入したのは、力学では2階微分までしか計算しないからであった(運動方程式は2階微分方程式なので、それ以上の高次の微分は計算しなくてよいのである)。ライプニッツは、実用的な運動方程式のみならず、より一般化した「力学」への発展を考えていたのかもしれない。そこでn階の微分が記述できる\(d^n/dx^n\)という記法を導入したのであろう。
さて、もとの計算に戻ると、xの微分、つまりfの微分は\(2\cos t - 2\sin 2t\)であるから、被積分関数は\[\begin{equation}g(t)\frac{df(t)}{dt}=2(2\cos t + \sin 2t)(\cos t - \sin 2t)\end{equation}\]である。これを展開するとかなり面倒な形となる。因子2を除いて計算すると
\[ \begin{equation} 2\cos^2 t -2\sin t \cos^2 t - 4 \cos^2 t ( 1-\cos^2 t) = -2\sin t \cos^2 t -2\cos^2 t + 4\cos^4 t\end{equation}\]
初項は\(k=\cos t\)と置換することで簡単に積分でき、\(\frac{2}{3}\cos^3 t\)となる。第二項は倍角の公式を使って\(-2\cos^2 t = -1-\cos 2t\)と変形すればよく、その積分は\(-t -\frac{1}{2}\sin 2t\)となる。最後の項は、\(4\cos^4 t = 4\left(\frac{1+\cos 2t}{2}\right)^2 = 1 + 2\cos 2t + \cos^2 2t\)であるが、\(\cos^2 2t = (1+\cos 4t)/2\)であるので、これを代入すると、\(\frac{3}{2} + 2\cos 2t +\frac{1}{2}\cos 4t\)である。その積分は\(\frac{3}{2}t +\sin 2t +\frac{1}{8}\sin 4t\)となる。以上の結果をまとめると
\[\int_0^{\frac{\pi}{2}} g(t)\frac{f(t)}{dt}dt = \left[\frac{4}{3}\cos^3 t +t + \sin 2t + \frac{1}{4}\sin 4t\right]_0^{\frac{\pi}{2}}=\frac{\pi}{2}-\frac{4}{3}\]
を得る。
それにしても、ここまでの計算は、「見てはならないもの(グラフの概形)」を見たから たどり着けたようなものである(鶴の恩返し?)。(gnuplotに頼らず)グラフの概形を簡単に得る方法はあるのだろうか?また、積分の計算をもう少し簡単に行う方法はあるのだろうか?
この辺りが、これからの課題であろう。
tの範囲を気にしないで、ぐるぐる回せばCは3回対称な図形になることは(gnuplotさえ使えれば)すぐにわかる。ただ、この問題ではtの範囲が0からπ/2までなので、図形の一部を考えなくてはならない。
\(0 \leqq t_1< t_2 \leqq \frac{\pi}{2}\)かつ、\(f(t_1)=f(t_2)\)が成り立つとき、\(g(t_1)^2 - g(t_2)^2 >0\)が成立することを示せ。
φが0から2π/3まで変化するとき、(x,y)はx軸上の点(-3,0)から、「棘の張り出し」に相当する点\((3/2, 3\sqrt{3}/2)\)まで滑らかに変化する。これをθ(つまりt)の範囲に直すと、-π/2からπ/6までに相当する。tは0からなので、この範囲ではまずい。t=0のとき、φ=π/2であるが、この点に対応するのが(1,2)である。
次は、φが2π/3から4π/3まで変化するときであるが、このときは点\((3/2,3\sqrt{3}/2)\)から、x軸に線対称な点\((3/2,-3\sqrt{3}/2)\)まで滑らかに変化する。この範囲はtでいうとπ/6から5π/6であるが、tはπ/2までであるから\(\frac{\pi}{6} \leqq t \leqq \frac{\pi}{2}\)である。t=π/2というのはφ=πの点で、x軸上の点(1,0)に相当する。
まとめると、\(0\leqq t \leqq \frac{\pi}{6}\)において(これを領域Iと呼ぼう)、Cは点(1,2)から点\((\frac{3}{2},\frac{3\sqrt{3}}{2})\)まで滑らかに変化する単調増加なグラフである。一方、\(\frac{\pi}{6}\leqq t \leqq \frac{\pi}{2}\)では(これを領域IIと呼ぼう)、Cは点\((\frac{3}{2},\frac{3\sqrt{3}}{2})\)から点(1,0)まで滑らかに変化する単調減少のグラフである。2つの領域を同時に考えると、\(1\leqq x \leqq \frac{3\sqrt{3}}{2}\)の領域でy=y(x)は二価関数となる(つまり、y=f(x)を考えた時、同じxに対して異なる2つのyの値が対応しているということで、グラフで考えるとx軸に対する垂線がyのグラフと異なる2箇所で交点をもつということ)。ただし、yやxをtの関数と見なせば、それぞれは一価関数である(同じxでも\(x=f(t_1)=f(t_2)\)となって、異なるtになっているということ)。
領域Iと領域IIをグラフで観察すると、その形から常に\(g(I) > g(II) > 0\)が成立しているのがわかる。 したがって、\(g(I)+g(II) > 0\)は自明であるので、上の関係を用いると\[\left\{g(I)+g(II)\right\}\left\{g(I)-g(II)\right\} > 0\]が成り立つのは自明である。領域Iと領域IIはtの立場からすると、\(t_1\)が属するのが領域I, \(t_2\)が属するのが領域IIであるから、題意は証明されたといってよい。つまり、\(f(t_1)=f(t_2)\)という条件は、Cの「二価性」から, \(t_1\)はIに、\(t_2\)はIIに属し、両者が同じ領域に属することはないことを保証する条件に相当している。この部分が読み取れれば、証明の残りの部分はまさに自明なのである。
ここまでくれば、(3)は簡単、と書こうと思ったが、この問題は実によく練られていて、まだ油断ができない。計算すべきは領域Iにおけるy(t)とx軸の間の面積から、領域IIにおけるy(t)とx軸の間の面積を引いたもの(差)である。したがって、
\[\begin{eqnarray}S &=&\int_1^{\frac{3\sqrt{3}}{2}}ydx - \int_1^{\frac{3\sqrt{3}}{2}}ydx \\ &=&\int_0^{\frac{\pi}{6}}g(t)\frac{dx}{dt}dt - \int^{\frac{\pi}{6}}_{\frac{\pi}{2}}g(t)\frac{dx}{dt}dt \\
&=&\int_0^{\frac{\pi}{6}}g(t)\frac{dx}{dt}dt +\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}g(t)\frac{dx}{dt}dt \\
&=&\int_{0}^{\frac{\pi}{2}}g(t)\frac{dx}{dt}dt \end{eqnarray}\]を計算すればよい。
ここで変数変換のために導入した\(dx = \frac{dx}{dt}dt\) という関係式だが、これはニュートンの微分記号x'に比べて、ライプニッツの微分記号dxの方が強力であることを示す、有名な一例である。ニュートンの記号は、計算における筆記量を削減してくれるので「便利」ではあるが、微分演算が通常の割り算や代数演算に従って変形できる性質を持つことを示してはくれないので発展性の観点からは「不便」なのである。また、ニュートンがy'とかy''という記号を導入したのは、力学では2階微分までしか計算しないからであった(運動方程式は2階微分方程式なので、それ以上の高次の微分は計算しなくてよいのである)。ライプニッツは、実用的な運動方程式のみならず、より一般化した「力学」への発展を考えていたのかもしれない。そこでn階の微分が記述できる\(d^n/dx^n\)という記法を導入したのであろう。
さて、もとの計算に戻ると、xの微分、つまりfの微分は\(2\cos t - 2\sin 2t\)であるから、被積分関数は\[\begin{equation}g(t)\frac{df(t)}{dt}=2(2\cos t + \sin 2t)(\cos t - \sin 2t)\end{equation}\]である。これを展開するとかなり面倒な形となる。因子2を除いて計算すると
\[ \begin{equation} 2\cos^2 t -2\sin t \cos^2 t - 4 \cos^2 t ( 1-\cos^2 t) = -2\sin t \cos^2 t -2\cos^2 t + 4\cos^4 t\end{equation}\]
初項は\(k=\cos t\)と置換することで簡単に積分でき、\(\frac{2}{3}\cos^3 t\)となる。第二項は倍角の公式を使って\(-2\cos^2 t = -1-\cos 2t\)と変形すればよく、その積分は\(-t -\frac{1}{2}\sin 2t\)となる。最後の項は、\(4\cos^4 t = 4\left(\frac{1+\cos 2t}{2}\right)^2 = 1 + 2\cos 2t + \cos^2 2t\)であるが、\(\cos^2 2t = (1+\cos 4t)/2\)であるので、これを代入すると、\(\frac{3}{2} + 2\cos 2t +\frac{1}{2}\cos 4t\)である。その積分は\(\frac{3}{2}t +\sin 2t +\frac{1}{8}\sin 4t\)となる。以上の結果をまとめると
\[\int_0^{\frac{\pi}{2}} g(t)\frac{f(t)}{dt}dt = \left[\frac{4}{3}\cos^3 t +t + \sin 2t + \frac{1}{4}\sin 4t\right]_0^{\frac{\pi}{2}}=\frac{\pi}{2}-\frac{4}{3}\]
を得る。
それにしても、ここまでの計算は、「見てはならないもの(グラフの概形)」を見たから たどり着けたようなものである(鶴の恩返し?)。(gnuplotに頼らず)グラフの概形を簡単に得る方法はあるのだろうか?また、積分の計算をもう少し簡単に行う方法はあるのだろうか?
この辺りが、これからの課題であろう。
2018年3月7日水曜日
阪大2018問題3:フーリエ級数展開もどき?(でも複素数で解く)
今年の東大の問題でも多かったのが、曲線や領域のパラメータ表示の問題だ。パラメータをうまく消去して軌跡の関係式を手に入れるために、ごちゃごちゃと解析的な計算を繰り返す、というのがこの問題の中心部分だが、それだけになってしまってはつまらない。
この問題でも、(x,y)が作る軌跡を考えることになるのだが、そのパラメータ表示がフーリエ級数展開もどきに見えるところが、ちょっと面白い。
\[ x=f(t) = 2\sin t + \cos 2t, \quad y=g(t) = 2\cos t + \sin 2t\]で与えられる曲線Cを考えようという問題である。ただし問題ではtに範囲が付いていて\(0\leqq t \leqq \pi/2\)となっているが、曲線Cの本当の「美しさ」を楽しむためにはtは2πまで回した方がいい。gnuplotで描画してみると、次の図のようになった。
正三角形を内側に凹ませたような図形である。多分、頂点と頂点の間の角度は120度になっているのであろう。このような「離散回転」がもつ対称性は、結晶の構造などの分析で重要になる。今考えている図形の場合は「三回対称性」を持っている。数学的には、点群の中の巡回群というものに相当する概念によって取り扱うことができる。
この図形で気になるのは、頂点の位置である。そして、対称の軸や点はどこにくるのか、そしてこの図形の面積である。試験中はgnuplotが使えないから、手計算だけで分析を進めていかなくてはならないのが辛いところだ。(出題者はこの形を知った上で問題を出しているから、すごく不公平に感じる....まあ、入試とはそういうものである。)
まずは、図の概形を知らぬふりをして、この問題を解いてみよう。
この小問は、図形Cが閉曲線になっているので、その存在範囲を調べよ、ということである。この情報は、面積を求める時の積分範囲に相当するから重要である。東大2018(問5)では、\(Q(u)=2z - z^2\)という式が出てきた。これをベクトル風に書くと
\[ \left(\begin{array}{c}x\\y\end{array}\right) = 2 \left(\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right) + \left(\begin{array}{c}\cos 2\theta\\ \sin 2\theta\end{array}\right)
\] である。一方、阪大のこの問題では右辺第一項に対応するところで、正弦と余弦がひっくり返った形ににはなっているが、ほぼ同じような形式である。正弦と余弦をひっくり返すには位相をπ/2だけずらせば良い。つまり、阪大の場合は
\[ \left(\begin{array}{c}x\\y\end{array}\right) = 2 \left(\begin{array}{c}-\cos(\theta+\frac{\pi}{2})\\ \sin(\theta+\frac{\pi}{2})\end{array}\right) + \left(\begin{array}{c}\cos 2\theta\\ \sin 2\theta\end{array}\right)
\]である。
問題ではθはtと書かれているので、tを時間(time)とみなすことにしよう。力学的に表現すれば、第一項は、周期が2π(振動数が1)の調和振動(単振動)であり、第二項は周期がπ(振動数が2)の調和振動を表す。つまり、周期の異なる2つの調和振動子の線形合成(重ね合わせ)であるから、フーリエ級数の一番簡単な場合に相当する。
角度依存性が第一項と第二項で異なっているのは、見通しが悪いので、統一してしまおう。すなわち、上式を書き直して、
\[ \left(\begin{array}{c}x\\y\end{array}\right) = -2 \left(\begin{array}{c}\cos(\theta+\frac{\pi}{2})\\ -\sin(\theta+\frac{\pi}{2})\end{array}\right) -\left(\begin{array}{c}\cos 2(\theta+\frac{\pi}{2})\\ \sin 2(\theta+\frac{\pi}{2})\end{array}\right)
\]とする。θ+π/2=φと置けば、この形式は東大の問題と(第二項の符号を除いて)よく似た形となる。すなわち、複素数表示で\(C(z)=-2z^*-z^2, z=e^{i\varphi}\)と表せる。
さて、我々は曲線Cの概形を知らないふりをしていても、やはりもう知ってしまっているのであるから、C(z)の絶対値を計算してみたくなるのである。ここから、最大値についての情報は手にはいるであろう。\[ |C(z)|^2 = |(-2z^*-z^2) |^2 = (-2z^*-z^2)(-2z^*-z^2)^* \\ = 4|z|^2+2(z^3*+(z^*)^3)+|z|^4 = 5+2(z^3+z^{*3})\]となる。|z|=1であることを利用した。最後の結果で、3次式(3次の多項式)になっているのがポイントである。ここから、冒頭で観測した「3回対称性」が出てくるのである!
このことをよりよく見るためには、極座標表示を代入して見ると
\[|C(z)|^2 = 5 + 4\cos 3\varphi\]という形を得る。最大値は\(3\varphi= 2k\pi\)のとき\((k=0, \pm 1, \pm 2, \cdots\))で、その値は9、すなわち\(|C(z)|\)の最大値は3である。図を見ると、これは正しいことが確認できる。つまり、\(\varphi=0, \pi/3, 2\pi/3\)の3点で最大値を周期的にとるのである。
面白いことに、\(\varphi=0\)の点は(x,y)座標では(-3, 0)に相当する。これは\(C(z)=-2z^*-z^2\)の負の符号によるものである。また、\(\varphi=2\pi/3\)の点は\((\frac{3}{2},\frac{3\sqrt{3}}{2})\)である。そして\(\varphi=4\pi/3\)の点は\((\frac{3}{2},-\frac{3\sqrt{3}}{2})\)となる。つまり、φの増加(反時計回り)に対して、対応する図形上の点(x,y)は時計回りに動いていく。これは\(2z^*\)の効果である。一方、\(z^2\)は時計回りに動いていくが、振幅(つまり絶対値)が、初項の2に比べて半分しかないため、その効果は半減する。しかし、両者の位相が一致した時に、干渉のように大きな重ね合わせが発生し、図でみるような「棘の張り出し」のような形になるのである。
出発点から、\(2z^*\)の点は時計回りに角速度1でまわり、\(z^2\)の点は反時計回りに角速度2で回る。時間をtで表すと、時間tにおける両者の角度は\(\varphi_0(t)=t, \varphi_1(t)=-2t\)と表せる。両者の角度の差は\(\varphi_0(t)-\varphi_1(t) = 3t\)だが、これが0となるときに上述した「干渉」が起きて、「棘の張り出し」が発生する。角度の差が0と書いたが、一般角に拡張すると、差が2πの整数倍のとき(つまり周回遅れのような状況)も角度は一致する。したがって、\(3t=2n\pi\)のときに「干渉」が発生する。これが、3回対称性の(力学的考察に基づく)起源である。
(1)の答えは、当然「干渉」に相当するときである。計算を逆に辿って、干渉発生時のθを求め、その場合のxの値とyの値を書き出せば良い。ちなみに、「逆干渉」の場合、つまり、振幅の符号が正反対になる場合の条件を調べれば、そこが原点からの距離の最小値、つまり図形の凹んだところ、がもとまるはずである。 干渉とか、逆干渉とかいう概念は波動力学、ひいては量子力学でも出てくるから、理論物理を目指すなら、よく慣れておいたほうがよいだろう。
以上は、図形の形がわかってしまった前提で解く方法だが、図形の概形を知るのは結構面倒である。図形を知らずにこの問題を特にはどうしたらよいだろうか?次の課題としたい。
この問題でも、(x,y)が作る軌跡を考えることになるのだが、そのパラメータ表示がフーリエ級数展開もどきに見えるところが、ちょっと面白い。
\[ x=f(t) = 2\sin t + \cos 2t, \quad y=g(t) = 2\cos t + \sin 2t\]で与えられる曲線Cを考えようという問題である。ただし問題ではtに範囲が付いていて\(0\leqq t \leqq \pi/2\)となっているが、曲線Cの本当の「美しさ」を楽しむためにはtは2πまで回した方がいい。gnuplotで描画してみると、次の図のようになった。
正三角形を内側に凹ませたような図形である。多分、頂点と頂点の間の角度は120度になっているのであろう。このような「離散回転」がもつ対称性は、結晶の構造などの分析で重要になる。今考えている図形の場合は「三回対称性」を持っている。数学的には、点群の中の巡回群というものに相当する概念によって取り扱うことができる。
この図形で気になるのは、頂点の位置である。そして、対称の軸や点はどこにくるのか、そしてこの図形の面積である。試験中はgnuplotが使えないから、手計算だけで分析を進めていかなくてはならないのが辛いところだ。(出題者はこの形を知った上で問題を出しているから、すごく不公平に感じる....まあ、入試とはそういうものである。)
まずは、図の概形を知らぬふりをして、この問題を解いてみよう。
(1) f(t)とg(t)の最大値を求めよ。ただし、\(0\leqq t \leqq \frac{\pi}{2}\)
この小問は、図形Cが閉曲線になっているので、その存在範囲を調べよ、ということである。この情報は、面積を求める時の積分範囲に相当するから重要である。東大2018(問5)では、\(Q(u)=2z - z^2\)という式が出てきた。これをベクトル風に書くと
\[ \left(\begin{array}{c}x\\y\end{array}\right) = 2 \left(\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right) + \left(\begin{array}{c}\cos 2\theta\\ \sin 2\theta\end{array}\right)
\] である。一方、阪大のこの問題では右辺第一項に対応するところで、正弦と余弦がひっくり返った形ににはなっているが、ほぼ同じような形式である。正弦と余弦をひっくり返すには位相をπ/2だけずらせば良い。つまり、阪大の場合は
\[ \left(\begin{array}{c}x\\y\end{array}\right) = 2 \left(\begin{array}{c}-\cos(\theta+\frac{\pi}{2})\\ \sin(\theta+\frac{\pi}{2})\end{array}\right) + \left(\begin{array}{c}\cos 2\theta\\ \sin 2\theta\end{array}\right)
\]である。
問題ではθはtと書かれているので、tを時間(time)とみなすことにしよう。力学的に表現すれば、第一項は、周期が2π(振動数が1)の調和振動(単振動)であり、第二項は周期がπ(振動数が2)の調和振動を表す。つまり、周期の異なる2つの調和振動子の線形合成(重ね合わせ)であるから、フーリエ級数の一番簡単な場合に相当する。
角度依存性が第一項と第二項で異なっているのは、見通しが悪いので、統一してしまおう。すなわち、上式を書き直して、
\[ \left(\begin{array}{c}x\\y\end{array}\right) = -2 \left(\begin{array}{c}\cos(\theta+\frac{\pi}{2})\\ -\sin(\theta+\frac{\pi}{2})\end{array}\right) -\left(\begin{array}{c}\cos 2(\theta+\frac{\pi}{2})\\ \sin 2(\theta+\frac{\pi}{2})\end{array}\right)
\]とする。θ+π/2=φと置けば、この形式は東大の問題と(第二項の符号を除いて)よく似た形となる。すなわち、複素数表示で\(C(z)=-2z^*-z^2, z=e^{i\varphi}\)と表せる。
さて、我々は曲線Cの概形を知らないふりをしていても、やはりもう知ってしまっているのであるから、C(z)の絶対値を計算してみたくなるのである。ここから、最大値についての情報は手にはいるであろう。\[ |C(z)|^2 = |(-2z^*-z^2) |^2 = (-2z^*-z^2)(-2z^*-z^2)^* \\ = 4|z|^2+2(z^3*+(z^*)^3)+|z|^4 = 5+2(z^3+z^{*3})\]となる。|z|=1であることを利用した。最後の結果で、3次式(3次の多項式)になっているのがポイントである。ここから、冒頭で観測した「3回対称性」が出てくるのである!
このことをよりよく見るためには、極座標表示を代入して見ると
\[|C(z)|^2 = 5 + 4\cos 3\varphi\]という形を得る。最大値は\(3\varphi= 2k\pi\)のとき\((k=0, \pm 1, \pm 2, \cdots\))で、その値は9、すなわち\(|C(z)|\)の最大値は3である。図を見ると、これは正しいことが確認できる。つまり、\(\varphi=0, \pi/3, 2\pi/3\)の3点で最大値を周期的にとるのである。
面白いことに、\(\varphi=0\)の点は(x,y)座標では(-3, 0)に相当する。これは\(C(z)=-2z^*-z^2\)の負の符号によるものである。また、\(\varphi=2\pi/3\)の点は\((\frac{3}{2},\frac{3\sqrt{3}}{2})\)である。そして\(\varphi=4\pi/3\)の点は\((\frac{3}{2},-\frac{3\sqrt{3}}{2})\)となる。つまり、φの増加(反時計回り)に対して、対応する図形上の点(x,y)は時計回りに動いていく。これは\(2z^*\)の効果である。一方、\(z^2\)は時計回りに動いていくが、振幅(つまり絶対値)が、初項の2に比べて半分しかないため、その効果は半減する。しかし、両者の位相が一致した時に、干渉のように大きな重ね合わせが発生し、図でみるような「棘の張り出し」のような形になるのである。
出発点から、\(2z^*\)の点は時計回りに角速度1でまわり、\(z^2\)の点は反時計回りに角速度2で回る。時間をtで表すと、時間tにおける両者の角度は\(\varphi_0(t)=t, \varphi_1(t)=-2t\)と表せる。両者の角度の差は\(\varphi_0(t)-\varphi_1(t) = 3t\)だが、これが0となるときに上述した「干渉」が起きて、「棘の張り出し」が発生する。角度の差が0と書いたが、一般角に拡張すると、差が2πの整数倍のとき(つまり周回遅れのような状況)も角度は一致する。したがって、\(3t=2n\pi\)のときに「干渉」が発生する。これが、3回対称性の(力学的考察に基づく)起源である。
(1)の答えは、当然「干渉」に相当するときである。計算を逆に辿って、干渉発生時のθを求め、その場合のxの値とyの値を書き出せば良い。ちなみに、「逆干渉」の場合、つまり、振幅の符号が正反対になる場合の条件を調べれば、そこが原点からの距離の最小値、つまり図形の凹んだところ、がもとまるはずである。 干渉とか、逆干渉とかいう概念は波動力学、ひいては量子力学でも出てくるから、理論物理を目指すなら、よく慣れておいたほうがよいだろう。
以上は、図形の形がわかってしまった前提で解く方法だが、図形の概形を知るのは結構面倒である。図形を知らずにこの問題を特にはどうしたらよいだろうか?次の課題としたい。
2018年3月6日火曜日
東大数学2018の全体的な感想
「理論物理学の考え方が楽しめるかどうか」という観点から見ると、今年の東大の数学の問題は面白みがあまりなかった。唯一楽しめたのは、複素数を扱った問題5。座標変換をうまく利用して、一見面倒に見える問題を簡易化して解く、という理論物理における常套手段を存分に使うことができた。
問題5では、x軸上に頂点を持つ「横倒し」になった放物線の方程式\(x=-y^2+\frac{1}{4}\)が、原点からの角度θを用いて\[x=-\frac{1}{2}\frac{\cos\theta}{1-\cos\theta}, \quad y= \frac{1}{2}\frac{\sin\theta}{1-\cos\theta}\]とパラメーター表示できることを学んだ。これはnon-trivialな表現だと思う。ある意味「発見」である。どこかでまた使えるかもしれない。
ちなみに、このパラメータ表現を\(-\pi/2\)だけ回転させたら、\(y=x^2+b\)のパラメータ表示が手に入るだろうか?ちょっと考えてみよう。まず対応する回転行列\(R(-\frac{\pi}{2})\)を計算してみる。\(\sin\frac{\pi}{2}=1, \cos\frac{\pi}{2}=0\)だから、
\[R(-\pi/2)=\left(\begin{array}{cc} 0 & 1 \\ -1 & 0\end{array}\right)\]である。\(x=-y^2+\frac{1}{4}\)上の点(x,y)を回転させて得た点の座標を(x',y')とすると、2つの点は線形変換
\[\left(\begin{array}{c} x' \\ y'\end{array}\right) = R(\pi/2)\left(\begin{array}{c} x \\ y\end{array}\right)\]
によって結ばれている。これを逆に解けば、xとyがx'とy'で記述された表式(具体的にはx=-y', y=x')が手に入り、これをもとの放物線に代入して整理すると、\(y'=x'^2-\frac{1}{4}\)を得る。つまり\(b=-1/4\)だったというわけで、予想通りである。パラメータ表示はしたがって、xとyに対応するものを交換すれば(片方の符号は変えねばならないが)それが、「通常の放物線」のパラメータ表示となるはずだ。すなわち、\(y=x^2-\frac{1}{4}\)のパラメータ表示は\[ x=\frac{1}{2}\frac{\sin\theta}{1-\cos\theta}, \quad y=\frac{1}{2}\frac{\cos\theta}{1-\cos\theta}\]となる。検算して見ると、たしかにこのパラメータ表示は、通常の放物線の方程式に対応していることが確認できる。ここで面白いのは、θが原点の周りの(x軸から測った)角度になっていることである。(放物線の焦点や凖線と呼ばれるものは、この場合はどこにくるか調べて見るのもおもしろいだろう。)この表現は、どこかで役に立つ日がくるだろう。こういうのは、頭の片隅に置いておくと、ある日、大きな発見につながるものである。
ところで、この問題で求めたQ(u)、すなわち円周上の接線P(z)に対し、A(1)と線対称な位置にくる点、の表現が、今年の阪大の問題3とよく似た表現になっている。なぜこんな偶然がおきるかというと、きっとこれは偶然ではなく、両者ともにフーリエ級数を念頭に問題を作っているからではないかと思われる。これに関しては、別の機会に検討してみよう。
東大の問題1では、テイラー展開や極限の考えを適用することができた。2つの極限を、例えば、x=0とx=+∞で考え、その両者の漸近形を中間領域でうまく結ぶ、という考え方は、プランクがその放射公式の導出で利用した、まさに現象論的な考え方である。ボルツマンの「離散化計算の癖」を踏襲した点は見過ごせないが、プランクが量子の概念にたどり着けたのは、この問題で考えたような方法論に従ったからである。問題の難易ではなく、このような観点から問題に向き合うことも、意外に大切なのではないだろうか?
問題2でも、漸近形の考察や現象論的な方法論が重要になった。理論物理では、こういう泥臭いやり方も多様するので、よく練習して習熟しておくとよいと思う。具体例をたくさん計算して、傾向を見抜き、そこから現象論的な法則を導いたり、原理を探ったりする、というこのやり方は、ファインマンが得意としたやり方である。最近、「ファインマン流物理がわかるコツ」という本を最近読み始めたのだが、これは落第寸前のカルテックの学生に向けて行われた補講の講義録である(カルテックのみならず、東大に入っても、かならず一定の割合で落第してしまう学生がいるのは、宇宙の普遍的な真理らしい)。この本の最初で「複雑な関数の微分を簡単に行うやり方」というのを彼は披露しているのだが、その方法は非常に独特で、どうしてそれが正しいか理解するには、実のところ、相当な知識と理解力が要求され、落第寸前の学生には到底わからないだろうと思う。が、彼が「落第寸前の学生を救うために」といいながらも、こういう「新しい計算法」を編み出しては自分が一番楽しんでしまっているのである。「計算を楽しむ」彼の一面(そしてそれは出来の悪い学生には非情である)がよくわかって、思わず笑ってしまったのである。
今年は、軌跡やその類を調べさせる問題がたくさんでた。問題3、4、5、6と、後半の問題はすべて関連している。ただ、問題3で見られたようにパラメータをただ単に消していくだけの問題は(理論物理の観点から見ると)つまらない。せっかくベクトルを持ち出しているのだから、もっと線形代数やベクトル空間の考え方をなぞるような問題にして欲しかった。こういう問題が「ベクトル」だと思われてしまうと、大学で物理学を教える立場からすると、非常に厄介である。高校の指導要領で歪んでしまった「高校生の頭」を、物理を学ぶ「大学生の頭」へと変えるのに、多大な労力が必要となるのである。ある意味、「優秀な」大学1年生ほど、頭がかちこちに固まっていて、そこからなかなか抜け出せず、「落第」していくのである....できるかぎり、高校の段階で、大学で学ぶような「普通の数学的感覚」を教えてあげてほしい。そのためには、東大の数学の問題は、指導要領に基づくのではなくて、出題者自らの研究内容をアレンジして作ってもらいたいのである。
ちなみに、確率の問題が今年は出なかったのは興味深い。量子力学の問題を組み込めたらよいのだが、場合の数の数えあげばかりでは、出題する方も飽きがくるというものである。波動関数がダメなら、ブラウン運動とかどうだろうか?つまり、ランダムウォークである。
問題5では、x軸上に頂点を持つ「横倒し」になった放物線の方程式\(x=-y^2+\frac{1}{4}\)が、原点からの角度θを用いて\[x=-\frac{1}{2}\frac{\cos\theta}{1-\cos\theta}, \quad y= \frac{1}{2}\frac{\sin\theta}{1-\cos\theta}\]とパラメーター表示できることを学んだ。これはnon-trivialな表現だと思う。ある意味「発見」である。どこかでまた使えるかもしれない。
ちなみに、このパラメータ表現を\(-\pi/2\)だけ回転させたら、\(y=x^2+b\)のパラメータ表示が手に入るだろうか?ちょっと考えてみよう。まず対応する回転行列\(R(-\frac{\pi}{2})\)を計算してみる。\(\sin\frac{\pi}{2}=1, \cos\frac{\pi}{2}=0\)だから、
\[R(-\pi/2)=\left(\begin{array}{cc} 0 & 1 \\ -1 & 0\end{array}\right)\]である。\(x=-y^2+\frac{1}{4}\)上の点(x,y)を回転させて得た点の座標を(x',y')とすると、2つの点は線形変換
\[\left(\begin{array}{c} x' \\ y'\end{array}\right) = R(\pi/2)\left(\begin{array}{c} x \\ y\end{array}\right)\]
によって結ばれている。これを逆に解けば、xとyがx'とy'で記述された表式(具体的にはx=-y', y=x')が手に入り、これをもとの放物線に代入して整理すると、\(y'=x'^2-\frac{1}{4}\)を得る。つまり\(b=-1/4\)だったというわけで、予想通りである。パラメータ表示はしたがって、xとyに対応するものを交換すれば(片方の符号は変えねばならないが)それが、「通常の放物線」のパラメータ表示となるはずだ。すなわち、\(y=x^2-\frac{1}{4}\)のパラメータ表示は\[ x=\frac{1}{2}\frac{\sin\theta}{1-\cos\theta}, \quad y=\frac{1}{2}\frac{\cos\theta}{1-\cos\theta}\]となる。検算して見ると、たしかにこのパラメータ表示は、通常の放物線の方程式に対応していることが確認できる。ここで面白いのは、θが原点の周りの(x軸から測った)角度になっていることである。(放物線の焦点や凖線と呼ばれるものは、この場合はどこにくるか調べて見るのもおもしろいだろう。)この表現は、どこかで役に立つ日がくるだろう。こういうのは、頭の片隅に置いておくと、ある日、大きな発見につながるものである。
ところで、この問題で求めたQ(u)、すなわち円周上の接線P(z)に対し、A(1)と線対称な位置にくる点、の表現が、今年の阪大の問題3とよく似た表現になっている。なぜこんな偶然がおきるかというと、きっとこれは偶然ではなく、両者ともにフーリエ級数を念頭に問題を作っているからではないかと思われる。これに関しては、別の機会に検討してみよう。
東大の問題1では、テイラー展開や極限の考えを適用することができた。2つの極限を、例えば、x=0とx=+∞で考え、その両者の漸近形を中間領域でうまく結ぶ、という考え方は、プランクがその放射公式の導出で利用した、まさに現象論的な考え方である。ボルツマンの「離散化計算の癖」を踏襲した点は見過ごせないが、プランクが量子の概念にたどり着けたのは、この問題で考えたような方法論に従ったからである。問題の難易ではなく、このような観点から問題に向き合うことも、意外に大切なのではないだろうか?
問題2でも、漸近形の考察や現象論的な方法論が重要になった。理論物理では、こういう泥臭いやり方も多様するので、よく練習して習熟しておくとよいと思う。具体例をたくさん計算して、傾向を見抜き、そこから現象論的な法則を導いたり、原理を探ったりする、というこのやり方は、ファインマンが得意としたやり方である。最近、「ファインマン流物理がわかるコツ」という本を最近読み始めたのだが、これは落第寸前のカルテックの学生に向けて行われた補講の講義録である(カルテックのみならず、東大に入っても、かならず一定の割合で落第してしまう学生がいるのは、宇宙の普遍的な真理らしい)。この本の最初で「複雑な関数の微分を簡単に行うやり方」というのを彼は披露しているのだが、その方法は非常に独特で、どうしてそれが正しいか理解するには、実のところ、相当な知識と理解力が要求され、落第寸前の学生には到底わからないだろうと思う。が、彼が「落第寸前の学生を救うために」といいながらも、こういう「新しい計算法」を編み出しては自分が一番楽しんでしまっているのである。「計算を楽しむ」彼の一面(そしてそれは出来の悪い学生には非情である)がよくわかって、思わず笑ってしまったのである。
今年は、軌跡やその類を調べさせる問題がたくさんでた。問題3、4、5、6と、後半の問題はすべて関連している。ただ、問題3で見られたようにパラメータをただ単に消していくだけの問題は(理論物理の観点から見ると)つまらない。せっかくベクトルを持ち出しているのだから、もっと線形代数やベクトル空間の考え方をなぞるような問題にして欲しかった。こういう問題が「ベクトル」だと思われてしまうと、大学で物理学を教える立場からすると、非常に厄介である。高校の指導要領で歪んでしまった「高校生の頭」を、物理を学ぶ「大学生の頭」へと変えるのに、多大な労力が必要となるのである。ある意味、「優秀な」大学1年生ほど、頭がかちこちに固まっていて、そこからなかなか抜け出せず、「落第」していくのである....できるかぎり、高校の段階で、大学で学ぶような「普通の数学的感覚」を教えてあげてほしい。そのためには、東大の数学の問題は、指導要領に基づくのではなくて、出題者自らの研究内容をアレンジして作ってもらいたいのである。
ちなみに、確率の問題が今年は出なかったのは興味深い。量子力学の問題を組み込めたらよいのだが、場合の数の数えあげばかりでは、出題する方も飽きがくるというものである。波動関数がダメなら、ブラウン運動とかどうだろうか?つまり、ランダムウォークである。
2018年3月5日月曜日
ベクトルの問題とは言えないベクトルの問題:東大2018(問3)
東大数学2018の問3は一見してベクトルの問題であるが、あまりベクトルの性質を使って解く問題ではないことがわかり、興味を失った。行列も使う必要がないように見える。
この「つまらなさ」は、パラメータkの逆数が問題に入り込んでいる点にあると思う。割り算という演算は、線形代数やベクトル空間とは親和性があまりないのだ。ベクトル空間や線形空間というのは、やはり「足し算」である(「引き算」も「足し算」に含まれる)。拡張的な内容としては、内積や外積などの「積」の定義をどうするか、というのもある。しかし、この問題ではこのようなテーマの切り口で解釈することはできなかった。残念である。
この問題はkが1/kの形で分母にあるのが邪魔である。そこで、早々と全てをk倍してしまって、「割り算」を消すところから始めることになる。まずは定義から
\[ \vec{OR} =\frac{1}{k}\left(\begin{array}{c} x \\ x^2\end{array}\right) + k\left(\begin{array}{c} t \\ 0\end{array}\right) \equiv \left(\begin{array}{c}X\\Y\end{array}\right) \]である。両辺にkをかけて、xを消去することにする。tというのは\(\vec{OA}\)のx座標であるが、Xにしか現れない。YとXの関係式を得るためには、両方の変数に関わるxを消去した方が便利であるのは明らかである。
この結果として、
\[
Y=k(X-kt)^2
\]
を得る。これは頂点(kt,0)、すなわちX軸に接した放物線である。tの範囲は0から1までだから、この放物線は0からkまで頂点がX軸上を移動することになる。また、Xの範囲はxとXの関係を逆に解いて
\[
kt - \frac{1}{k} \leq X \leq kt + \frac{1}{k}
\]
となる。tを動かしながら、これらの情報をうまく利用して\(S(k)\)を求めれば、この問題はそれほど難しくない。
以上のことから、一次変換も、線形独立性も、考える必要がないので、この問題は単なるパラメータを消す練習としか解釈できなかった。理論物理学の観点からは「残念な問題」であった。
ちなみに、続く問4も素直にやれば解ける問題であり、 高校数学の発想の範囲内でやるだけであろう。やる気が失せたので、こちらも省略。問6は空間の認識のトレーニングであるが、少し捻って2次方程式の問題に持ち込めるかなという希望がちょっとあったのだが、結局は球を引きずり回すだけの話に落ち着いてしまい、理論物理学の考え方を持ち込む余地はあまりなかった。これも省略。
この「つまらなさ」は、パラメータkの逆数が問題に入り込んでいる点にあると思う。割り算という演算は、線形代数やベクトル空間とは親和性があまりないのだ。ベクトル空間や線形空間というのは、やはり「足し算」である(「引き算」も「足し算」に含まれる)。拡張的な内容としては、内積や外積などの「積」の定義をどうするか、というのもある。しかし、この問題ではこのようなテーマの切り口で解釈することはできなかった。残念である。
この問題はkが1/kの形で分母にあるのが邪魔である。そこで、早々と全てをk倍してしまって、「割り算」を消すところから始めることになる。まずは定義から
\[ \vec{OR} =\frac{1}{k}\left(\begin{array}{c} x \\ x^2\end{array}\right) + k\left(\begin{array}{c} t \\ 0\end{array}\right) \equiv \left(\begin{array}{c}X\\Y\end{array}\right) \]である。両辺にkをかけて、xを消去することにする。tというのは\(\vec{OA}\)のx座標であるが、Xにしか現れない。YとXの関係式を得るためには、両方の変数に関わるxを消去した方が便利であるのは明らかである。
この結果として、
\[
Y=k(X-kt)^2
\]
を得る。これは頂点(kt,0)、すなわちX軸に接した放物線である。tの範囲は0から1までだから、この放物線は0からkまで頂点がX軸上を移動することになる。また、Xの範囲はxとXの関係を逆に解いて
\[
kt - \frac{1}{k} \leq X \leq kt + \frac{1}{k}
\]
となる。tを動かしながら、これらの情報をうまく利用して\(S(k)\)を求めれば、この問題はそれほど難しくない。
以上のことから、一次変換も、線形独立性も、考える必要がないので、この問題は単なるパラメータを消す練習としか解釈できなかった。理論物理学の観点からは「残念な問題」であった。
ちなみに、続く問4も素直にやれば解ける問題であり、 高校数学の発想の範囲内でやるだけであろう。やる気が失せたので、こちらも省略。問6は空間の認識のトレーニングであるが、少し捻って2次方程式の問題に持ち込めるかなという希望がちょっとあったのだが、結局は球を引きずり回すだけの話に落ち着いてしまい、理論物理学の考え方を持ち込む余地はあまりなかった。これも省略。
整数問題における極限の利用:東大2018(問2)
東大数学2018の問2を見てみよう。これも簡単な問題ではあるが、方針が定まるまでは色々と試して見なくてはならないだろう。
(1)は簡単で、すぐに\(q_n/p_n = \frac{2(2n+1)}{n(n+1)}\)であることが計算できる。細かいチェックは必要だと思うので、答案にはそういうのも書き込んでおく必要があろう。が、ここでは省略する。大切なことは、分母を2で割っておく必要があるということである。つまり、分子に出た2を、分母で1/2と書きあらわす必要があるということである。これはnが偶数のときと、奇数の時に分けて考えれば明らかとなる。すなわち、
\[
\frac{q_{2k}}{p_{2k}} = \frac{4k+1}{k(2k+1)}, \quad
\frac{q_{2k-1}}{p_{2k-1}} = \frac{4k-1}{k(2k-1)}
\]
(2)に移ろう。理論物理でいう「現象論」のアプローチを取ってみる。つまり、いくつか実例を観察してみて、その上で「現象論的な法則」を見つけ出すというやり方である。簡単にいうと、数列をいくつか計算してみるのである。
\(a_1=3, a_2=5, a_3=35/6 = 5.8..., a_4=21/4=5.25, a_5=77/20 = 3.8..., \\ a_6=143/60 = 2.38..., a_7=143/112 = 1.27..., a_8=2431/4032 < 1, \cdots\)
という結果となる。
最初の2つが整数値を取り、あとは分数になるように見える。 グラフにまとめてみると、下のようになった。
大事な点は、\(a_n\)が一旦分数の値を取り始めた\(n=3\)以上では、数列の値が単調減少しているように見えることだ。これが本当かどうか調べてみよう。n番目とn-1番目の数列の要素の関係は、
\[
a_n=\left(\frac{q_n}{p_n}\right)a_{n-1} = \frac{2n+1}{n(n+1)/2}a_{n-1}
\]
である。nが大きな値をとった時の\(q_n/p_n\)の漸近形は
\[
\frac{q_n}{p_n}=\frac{2+\frac{1}{n}}{\frac{n}{2}\left(1+\frac{1}{n}\right)} \rightarrow \frac{4}{n}
\]
である。上のグラフで4/xのグラフ(緑色)を重ねたのは、これが\(q_n/p_n\)の漸近形となっているからである。実際n=8付近でよく両者は一致しているのが確認できる。
数列\(a_1, a_2,\cdots\)を\[a_n= \frac{_{2n+1}C_n}{n!} \quad (n=1,2,\cdots)\]で定める。
(1) \(n\geqq 2\)とする。\(\frac{a_n}{a_{n-1}}\)を既約分数\(\frac{q_n}{p_n}\)として表したときの分母\(p_n \geqq 1\)と分子\(q_n\)を求めよ。
(2)\(a_n\)が整数となる\(n\geqq 1\)をすべて求めよ。
(1)は簡単で、すぐに\(q_n/p_n = \frac{2(2n+1)}{n(n+1)}\)であることが計算できる。細かいチェックは必要だと思うので、答案にはそういうのも書き込んでおく必要があろう。が、ここでは省略する。大切なことは、分母を2で割っておく必要があるということである。つまり、分子に出た2を、分母で1/2と書きあらわす必要があるということである。これはnが偶数のときと、奇数の時に分けて考えれば明らかとなる。すなわち、
\[
\frac{q_{2k}}{p_{2k}} = \frac{4k+1}{k(2k+1)}, \quad
\frac{q_{2k-1}}{p_{2k-1}} = \frac{4k-1}{k(2k-1)}
\]
(2)に移ろう。理論物理でいう「現象論」のアプローチを取ってみる。つまり、いくつか実例を観察してみて、その上で「現象論的な法則」を見つけ出すというやり方である。簡単にいうと、数列をいくつか計算してみるのである。
\(a_1=3, a_2=5, a_3=35/6 = 5.8..., a_4=21/4=5.25, a_5=77/20 = 3.8..., \\ a_6=143/60 = 2.38..., a_7=143/112 = 1.27..., a_8=2431/4032 < 1, \cdots\)
という結果となる。
最初の2つが整数値を取り、あとは分数になるように見える。 グラフにまとめてみると、下のようになった。
 |
| 横軸はn。紫の線は\(a_n\)、水色が\(q_n/p_n\)、緑が\(4/n\)に対応。 |
\[
a_n=\left(\frac{q_n}{p_n}\right)a_{n-1} = \frac{2n+1}{n(n+1)/2}a_{n-1}
\]
である。nが大きな値をとった時の\(q_n/p_n\)の漸近形は
\[
\frac{q_n}{p_n}=\frac{2+\frac{1}{n}}{\frac{n}{2}\left(1+\frac{1}{n}\right)} \rightarrow \frac{4}{n}
\]
である。上のグラフで4/xのグラフ(緑色)を重ねたのは、これが\(q_n/p_n\)の漸近形となっているからである。実際n=8付近でよく両者は一致しているのが確認できる。
\(n\gg 4\)のとき、\(q_n/p_n\)は1より小さいので、\(a_n < a_{n-1}\)であることが証明できる。つまり、nが大きいところで、この数列は単調減少なのである。問題はどのnからが「十分大きいn」なのかどうか、という判断である。
この判断をしやすくするために、\(q_n/p_n\)を下のように書き換えてみる。\[\frac{2(2n+1)}{n(n+1)} = 2 \frac{2(n+1)-1}{n(n+1)} = \frac{4}{n} - \frac{2}{n(n+1)} = \frac{2}{n}\left(2-\frac{1}{n+1}\right)\]
最後の等式のところに着目する。\(2-1/(n+1)\)というのは単調増加な双曲線上にあり、大きなnに対し2に収束する。n=4を代入してみると1.8という値を与えるので、\(n\geq 4\)において、ほぼ2に近い値を持ち続けることになる。そこで\(n\geq 4\) において
\[1.8 < 2-\frac{1}{n+1} < 2\]
となるので、この結果を\(q_n/p_n\)に代入すると、
\[\frac{3.6}{n} < q_n/p_n < \frac{4}{n}\]
の範囲で近似できる。いずれにしても、これは単調減少な数列である。
\(q_4/p_4 = 9/10 < 1\)だから、n=4より大きなところで数列は単調減少となることがわかる。つまり、「大きなn」というのは「4以上のn」ということなのであった。
最後のポイントは、数列自体の値が1より小さくなるのはどこか、ということである。数列の値が1より小さくなれば、そこより大きなnにおいて数列は1より小さな分数となるから、整数となることは2度とありえない。上の「現象論的計算」によれば、数列が1を切るのはn=8のときである。したがって、n=8より大きなときは整数となる数列は存在しないのである。
n=7以下の場合で数列が整数になるのは、計算によりn=1,2の2つの場合だけである。したがって、これが答えになる。
テイラー展開で解く:東大2018(問1)
2013年の阪大の問題で使ったテイラー展開を、今年の東大の問題でも使ってみよう。
テイラー展開は大学の物理でよく使う。例えば、\(g\)を重力定数、\(l\)を振り子の糸の長さとすると、振り子運動を記述する運動方程式は
\[
\frac{d^2\theta}{dt^2} = - \frac{g}{l}\sin\theta
\]となるが、振り子の振角θが微小であるとき(つまり\(|\theta|\ll 1\))、「調和振動子」に近似することができる。調和振動子とは、大雑把にいうと、バネのような復元力による周期運動のことで、力学はもちろん量子力学で重要な役割を果たす。上式の微分方程式で表される調和振動子の解は三角関数となる(後述する)。ちなみに、微小近似が使えないような大きな振幅で運動する場合は、上の微分方程式の解として、三角関数よりも複雑な「楕円関数」というものを導入しなくてはならない。
この「微小振動近似」のときに使う近似が、
\[
\sin\theta \simeq \theta \quad \cdots [A]
\]
というものである。この近似は正弦関数のテイラー展開
\[
\sin\theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} + \cdots \quad [B]
\]
によって正当化できる(このテイラー展開はθ=0周辺の展開となっているので、マクローリン展開と呼ばれるときもある)。余弦関数のテイラー展開は、上式の両辺を微分することで(形式的に)得ることができて、
\[
\cos\theta = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} + \cdots \quad [C]
\]
となる。
上の式の右辺のような無限和は、べき(冪)級数(すなわち、θの冪関数\(\theta^n\)の無限和)と呼ばれる。冪関数よりも複雑な関数、たとえば三角関数や指数関数など、を冪級数で表す(「展開する」という)とき、この級数のことをテイラー展開(あるいはテイラー級数展開)という。
つまり、近似式[A]は、正弦関数をテイラー展開したとき(最初の等号)、θが小さいという条件の下で、3次以上の高次項は、1次の項に比べて無視できるほと小さいと見なせるという意味である。近似式[A]を用いれば、微小振動の場合の振り子の運動方程式は、テイラー展開に基づく近似によって
\[
\frac{d^2\theta}{dt^2} = -\frac{g}{l}\theta
\]
と近似できる。これが「調和振動子」の運動方程式である。解が三角関数\(\theta(t)=A\cos(\omega t+\delta)\)であることは、代入してみればすぐにわかる。ただし、\(A, \delta\)は定数であり、\(\omega = \sqrt{\frac{g}{l}}\)である。
Taylor展開を行う御利益は、上の例をみても明らかであるが、次の通りである。冪関数ほど解析的に扱いが簡単な関数はないわけで、三角関数や指数関数などの「複雑な」関数の性質を、冪級数で表し、関連する計算や理論を簡易化しようというのである。(\(\sin x\)が\(x\)で近似できたら、問題は劇的に簡易化するのは自明であろう!)こうなると、問題の焦点は展開/級数の収束性に移ってくる。実際、大学に入って解析の講義を受けると、収束判定条件などについて学ぶことになる。
ちなみに、無限に続くこのような和(すなわち級数)で表される関数のことを超越関数(transcendental function)という。つまり、三角関数も指数関数も超越関数である。一方、冪関数の有限和は「多項式」という(高校数学では、なぜか「整式」という)。多項式と超越関数の違いは、有限和と無限和の違いであり、この違いが量子力学で大きな役割を果たす(例えば、1次元調和振動子のエネルギーが量子化され、対応する波動関数がエルミート多項式となるのは、無限和だと思っていたものが、実は有限和でなければならぬという条件、より正確には波動関数が発散せず二乗可積分であるべし、という条件から決まる)。
さて、この問題(問1)で扱うのは次の関数である。
\[
f(x) = \frac{x}{\sin x} + \cos x, \quad (0<x<\pi)
\]
三角関数のテイラー展開、式[B][C]を代入すると、
\[
f(x)= \frac{x}{x-\frac{x^3}{3!} + \cdots} + 1-\frac{x^2}{2!} + \cdots
= \left( 1 - \frac{x^2}{3!} + \cdots\right)^{-1} + 1 - \frac{x^2}{2!} + \cdots
\]
上の式をつかって\(\displaystyle \lim_{x\rightarrow +0}f(x)\)を計算するのは簡単である(答えは2)。これがテイラー展開の強みである。冪級数で表せば、複雑な関数の解析的な性質が簡易化するのである。
上式をさらに「簡易化」するために、\(g(x)=(1+x)^n\)のテイラー展開を考える。nが整数のときは二項展開が利用できるが、より一般の場合に拡張するのはそれほど難しくない。結論だけまとめると、
\[
g(x)=1+nx + \frac{n(n-1)}{2}x^2 + \cdots
\]
となる。
この「二項展開」のテイラー展開を利用して、f(x)のテイラー展開の負べきの部分を近似すると
\[
f(x) = \left( 1 +\frac{x^2}{3!} - \cdots\right) + \left(1 - \frac{x^2}{2!} + \cdots\right)
\]
となる。\(|x|\ll 1\)であることを使って、2次関数で近似すると
\[
f(x) \simeq 2 + \left(\frac{1}{3!}-\frac{1}{2!}\right) x^2
\]
を得る。これは頂点が(0,2)の、上に凸の放物線である。x→+0の極限が2であることがすぐにわかるし、f(x)の解析的な性質がx=0の周辺でどんな感じになっているか直感的に理解することができる。
今度は\(x=\pi\)周辺のテイラー展開を考える。xの範囲はπまでなので\(x=\pi - \xi\)と置く。ただし\(0<\xi\ll 1\)とする。f(x)は\(\xi\)の関数になるので\(f(x)\rightarrow f(\xi)\)と書き直すことにする。すなわち、
\[
f(x) = \frac{\pi-\xi}{\sin(\pi-\xi)} + \cos(\pi-\xi) = \frac{\pi - \xi}{\sin\xi} - \cos\xi \equiv f(\xi)
\]
である。\(\xi\)についてテイラー展開すると、
\[
f(\xi) = \left(\pi - \xi\right)\left( \xi - \frac{\xi^3}{3!} + \cdots\right)^{-1} + \left(1-\frac{\xi^2}{2!}+\cdots\right)
\]
\(\sin\xi\)を分母で展開した部分に、二項展開のテイラー展開を適用するために、\(\xi\)で括りだし、
\[
f(\xi) = \left(\frac{\pi}{\xi} - 1\right) \left( 1 - \frac{\xi^2}{3!}+\cdots\right)^{-1} + \left(1-\frac{\xi^2}{2!}+\cdots\right) \\ \simeq \left(\frac{\pi}{\xi} - 1\right) \left( 1 + \frac{\xi^2}{3!}-\cdots\right) + \left(1-\frac{\xi^2}{2!}+\cdots\right)
\]
とする。\(\xi\)は微小量であるから、1と比較して無視できる。したがって、\(\xi\rightarrow 0\)の極限において、\(f(\xi)\)は双曲線関数
\[
f(\xi) \simeq \frac{\pi}{\xi}
\]
のように振る舞うことがわかる。つまり\(x\rightarrow \pi - 0\)の極限でf(x)は+∞に発散することがわかる。また、\(f(\xi)\)の二階微分は\(f''(\xi)=2\xi^{-3}\)なので、\(\xi = +0\)で正値を取る。つまり、大雑把に言って「下に凸」のグラフとなる。
\(x=+0\)付近で上に凸の放物線、\(x=\pi-0\)付近で下に凸の双曲線でよく近似されるf(x)であるから、この2つのグラフをxの中間領域でなめらかに繋ぐには変曲点が少なくとも1つ(より正確には奇数個)は存在しているはずである。とすると、極値点というよりも極小点が一つは存在するだろう、という予想が立つ。f'(x)を計算すると\(x=\pi/2\)に極小点があることがわかる。x=0付近のテイラー展開(放物線)と、x=π付近のテイラー展開(双曲線)とをグラフにプロットすると、次の図のようになる。
極小点はx=π/2であるが、その付近でテイラー展開はオリジナルの関数f(x)から大きくずれていることがわかる。ここで曲率が変わらないと、2つのグラフがなめらかにつながらないからだが、放物線も双曲線も曲率は一定のままであるから、f(x)からずれていくのである。
極値がx=π/2以外では発生しないことを、きちんと証明するには、\(x>0\)の領域で、\(\sin x - x < 0\)が常に成り立つことを示す必要があるが、これは簡単にできるのでここでは割愛したい。
テイラー展開は大学の物理でよく使う。例えば、\(g\)を重力定数、\(l\)を振り子の糸の長さとすると、振り子運動を記述する運動方程式は
\[
\frac{d^2\theta}{dt^2} = - \frac{g}{l}\sin\theta
\]となるが、振り子の振角θが微小であるとき(つまり\(|\theta|\ll 1\))、「調和振動子」に近似することができる。調和振動子とは、大雑把にいうと、バネのような復元力による周期運動のことで、力学はもちろん量子力学で重要な役割を果たす。上式の微分方程式で表される調和振動子の解は三角関数となる(後述する)。ちなみに、微小近似が使えないような大きな振幅で運動する場合は、上の微分方程式の解として、三角関数よりも複雑な「楕円関数」というものを導入しなくてはならない。
この「微小振動近似」のときに使う近似が、
\[
\sin\theta \simeq \theta \quad \cdots [A]
\]
というものである。この近似は正弦関数のテイラー展開
\[
\sin\theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} + \cdots \quad [B]
\]
によって正当化できる(このテイラー展開はθ=0周辺の展開となっているので、マクローリン展開と呼ばれるときもある)。余弦関数のテイラー展開は、上式の両辺を微分することで(形式的に)得ることができて、
\[
\cos\theta = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} + \cdots \quad [C]
\]
となる。
上の式の右辺のような無限和は、べき(冪)級数(すなわち、θの冪関数\(\theta^n\)の無限和)と呼ばれる。冪関数よりも複雑な関数、たとえば三角関数や指数関数など、を冪級数で表す(「展開する」という)とき、この級数のことをテイラー展開(あるいはテイラー級数展開)という。
つまり、近似式[A]は、正弦関数をテイラー展開したとき(最初の等号)、θが小さいという条件の下で、3次以上の高次項は、1次の項に比べて無視できるほと小さいと見なせるという意味である。近似式[A]を用いれば、微小振動の場合の振り子の運動方程式は、テイラー展開に基づく近似によって
\[
\frac{d^2\theta}{dt^2} = -\frac{g}{l}\theta
\]
と近似できる。これが「調和振動子」の運動方程式である。解が三角関数\(\theta(t)=A\cos(\omega t+\delta)\)であることは、代入してみればすぐにわかる。ただし、\(A, \delta\)は定数であり、\(\omega = \sqrt{\frac{g}{l}}\)である。
Taylor展開を行う御利益は、上の例をみても明らかであるが、次の通りである。冪関数ほど解析的に扱いが簡単な関数はないわけで、三角関数や指数関数などの「複雑な」関数の性質を、冪級数で表し、関連する計算や理論を簡易化しようというのである。(\(\sin x\)が\(x\)で近似できたら、問題は劇的に簡易化するのは自明であろう!)こうなると、問題の焦点は展開/級数の収束性に移ってくる。実際、大学に入って解析の講義を受けると、収束判定条件などについて学ぶことになる。
ちなみに、無限に続くこのような和(すなわち級数)で表される関数のことを超越関数(transcendental function)という。つまり、三角関数も指数関数も超越関数である。一方、冪関数の有限和は「多項式」という(高校数学では、なぜか「整式」という)。多項式と超越関数の違いは、有限和と無限和の違いであり、この違いが量子力学で大きな役割を果たす(例えば、1次元調和振動子のエネルギーが量子化され、対応する波動関数がエルミート多項式となるのは、無限和だと思っていたものが、実は有限和でなければならぬという条件、より正確には波動関数が発散せず二乗可積分であるべし、という条件から決まる)。
さて、この問題(問1)で扱うのは次の関数である。
\[
f(x) = \frac{x}{\sin x} + \cos x, \quad (0<x<\pi)
\]
三角関数のテイラー展開、式[B][C]を代入すると、
\[
f(x)= \frac{x}{x-\frac{x^3}{3!} + \cdots} + 1-\frac{x^2}{2!} + \cdots
= \left( 1 - \frac{x^2}{3!} + \cdots\right)^{-1} + 1 - \frac{x^2}{2!} + \cdots
\]
上の式をつかって\(\displaystyle \lim_{x\rightarrow +0}f(x)\)を計算するのは簡単である(答えは2)。これがテイラー展開の強みである。冪級数で表せば、複雑な関数の解析的な性質が簡易化するのである。
上式をさらに「簡易化」するために、\(g(x)=(1+x)^n\)のテイラー展開を考える。nが整数のときは二項展開が利用できるが、より一般の場合に拡張するのはそれほど難しくない。結論だけまとめると、
\[
g(x)=1+nx + \frac{n(n-1)}{2}x^2 + \cdots
\]
となる。
この「二項展開」のテイラー展開を利用して、f(x)のテイラー展開の負べきの部分を近似すると
\[
f(x) = \left( 1 +\frac{x^2}{3!} - \cdots\right) + \left(1 - \frac{x^2}{2!} + \cdots\right)
\]
となる。\(|x|\ll 1\)であることを使って、2次関数で近似すると
\[
f(x) \simeq 2 + \left(\frac{1}{3!}-\frac{1}{2!}\right) x^2
\]
を得る。これは頂点が(0,2)の、上に凸の放物線である。x→+0の極限が2であることがすぐにわかるし、f(x)の解析的な性質がx=0の周辺でどんな感じになっているか直感的に理解することができる。
今度は\(x=\pi\)周辺のテイラー展開を考える。xの範囲はπまでなので\(x=\pi - \xi\)と置く。ただし\(0<\xi\ll 1\)とする。f(x)は\(\xi\)の関数になるので\(f(x)\rightarrow f(\xi)\)と書き直すことにする。すなわち、
\[
f(x) = \frac{\pi-\xi}{\sin(\pi-\xi)} + \cos(\pi-\xi) = \frac{\pi - \xi}{\sin\xi} - \cos\xi \equiv f(\xi)
\]
である。\(\xi\)についてテイラー展開すると、
\[
f(\xi) = \left(\pi - \xi\right)\left( \xi - \frac{\xi^3}{3!} + \cdots\right)^{-1} + \left(1-\frac{\xi^2}{2!}+\cdots\right)
\]
\(\sin\xi\)を分母で展開した部分に、二項展開のテイラー展開を適用するために、\(\xi\)で括りだし、
\[
f(\xi) = \left(\frac{\pi}{\xi} - 1\right) \left( 1 - \frac{\xi^2}{3!}+\cdots\right)^{-1} + \left(1-\frac{\xi^2}{2!}+\cdots\right) \\ \simeq \left(\frac{\pi}{\xi} - 1\right) \left( 1 + \frac{\xi^2}{3!}-\cdots\right) + \left(1-\frac{\xi^2}{2!}+\cdots\right)
\]
とする。\(\xi\)は微小量であるから、1と比較して無視できる。したがって、\(\xi\rightarrow 0\)の極限において、\(f(\xi)\)は双曲線関数
\[
f(\xi) \simeq \frac{\pi}{\xi}
\]
のように振る舞うことがわかる。つまり\(x\rightarrow \pi - 0\)の極限でf(x)は+∞に発散することがわかる。また、\(f(\xi)\)の二階微分は\(f''(\xi)=2\xi^{-3}\)なので、\(\xi = +0\)で正値を取る。つまり、大雑把に言って「下に凸」のグラフとなる。
\(x=+0\)付近で上に凸の放物線、\(x=\pi-0\)付近で下に凸の双曲線でよく近似されるf(x)であるから、この2つのグラフをxの中間領域でなめらかに繋ぐには変曲点が少なくとも1つ(より正確には奇数個)は存在しているはずである。とすると、極値点というよりも極小点が一つは存在するだろう、という予想が立つ。f'(x)を計算すると\(x=\pi/2\)に極小点があることがわかる。x=0付近のテイラー展開(放物線)と、x=π付近のテイラー展開(双曲線)とをグラフにプロットすると、次の図のようになる。
 |
| 紫色のグラフがオリジナルのf(x)のグラフ。緑色がx=0でテイラー展開した結果の放物線、水色はx=π付近で展開した結果の双曲線。それぞれの点で展開した結果は、それぞれの点の付近でよくオリジナルの関数と一致している。極小点はπ/2=1.57...あたりに発生しているように見え、その付近で2つのグラフは接続している。 |
極値がx=π/2以外では発生しないことを、きちんと証明するには、\(x>0\)の領域で、\(\sin x - x < 0\)が常に成り立つことを示す必要があるが、これは簡単にできるのでここでは割愛したい。
2018年2月26日月曜日
オイラーの公式で解く東大2018問5(2)
前半(1)に引き続き、「難」と評価された2018年の問5の後半(2)に取り組もう。
まず\(w=1/(1-u)\)をzで表しておこう。(1)の結果を使うと、
\[
w=\frac{1}{1-u} = \frac{1}{1-2z+z^2} = (z-1)^{-2}
\]
を得る。\(w=x+iy\)と表した時、xとyの関係がわかれば軌跡R(w)が手に入る。複素共役\(w^*=x-iy\)を使ってx,yを表すと、
\[
x=\frac{w+w^*}{2}, \quad y = \frac{w-w^*}{2i}
\]
である。この式と上の式を使えば、(x,y)を\(z=\cosθ+i\sinθ\)によって表すことができる。ちょっと長めの計算になるが、注意深く行うと、
\[
x=-\frac{1}{2}\frac{\cos\theta}{1-\cos\theta}, \quad y = \frac{1}{2}\frac{\sin\theta}{1-\cos\theta} \ \cdots [A]
\]という関係が手にはいる。この部分で使うのはオイラーの公式で得られる次の有名な恒等式である。
\[
\cos\theta = \frac{e^{i\theta}+e^{-i\theta}}{2}, \quad \sin\theta = \frac{e^{i\theta}-e^{-i\theta}}{2i}
\]
また、上の結果を使って得られる、次の計算結果も役にたつ。
\[
(e^{i\theta}-1) (e^{-i\theta}-1) = 2(1-\cos\theta)
\]
xとcosθの関係式を逆に解いて、cosθをxで表すと\(\cos\theta = -\frac{2x}{1-2x}\)となる。この結果を用いて、次にyとsinθの関係を計算することができる。結果は\(y=-\frac{2x-1}{2}\sin\theta\)である。\(\cos^2\theta+\sin^2\theta=1\)の関係式を用いるとθを消去することができて、
\[
\frac{4x^2}{(2x-1)^2} + \frac{4y^2}{(2x-1)^2} = 1
\]となる。これを整理すると
\[
x=-y^2 + \frac{1}{4}
\]を得る。つまり、軌跡はx軸方向に倒れた放物線である。
さて、問題となるのは、答えとなる軌跡Rはこの放物線全体ではないという点である。PはC’の上を動くだけであるので、θの範囲を\(\frac{\pi}{3}\le \theta \le \frac{5\pi}{3}\)に限らなければならない。
ちなみに、5つ上の式(式[A])を用いてgnuplotでパラメータ表示すると、下の図のようになる(これが答えである)。
式[A]を見ると、xはcosθのみで表されているから偶関数である。θの定義域の対称性と、θの関数としてのxの対称性を考えれば、θ=πのときにx=1/4となって放物線の頂点に対応することがわかる。したがって、θ=π/3, 5π/3の時にx=-1/2となり、ここがxの最小値である。つまり、xの範囲は\(-\frac{1}{2}\le x \le \frac{1}{4}\)である。一方、式[A]をみるとyは奇関数であり、対応するyの値は\(y=\pm\sqrt{3}/2\)である。
オイラーの公式を使うと(代数の計算はちょっと面倒になるが)、この手の問題は簡単に解くことができた。個人的には、この問題は「難」どころか「易」に感じる。というのも、上の解答をみたらわかるように、これは三角関数を含む代数計算の練習問題に過ぎない。
(2)Cのうち実部が1/2以下の複素数で表される部分をC’とする。点P(z)がC'上を動くときの点R(w)の軌跡を求めよ。
まず\(w=1/(1-u)\)をzで表しておこう。(1)の結果を使うと、
\[
w=\frac{1}{1-u} = \frac{1}{1-2z+z^2} = (z-1)^{-2}
\]
を得る。\(w=x+iy\)と表した時、xとyの関係がわかれば軌跡R(w)が手に入る。複素共役\(w^*=x-iy\)を使ってx,yを表すと、
\[
x=\frac{w+w^*}{2}, \quad y = \frac{w-w^*}{2i}
\]
である。この式と上の式を使えば、(x,y)を\(z=\cosθ+i\sinθ\)によって表すことができる。ちょっと長めの計算になるが、注意深く行うと、
\[
x=-\frac{1}{2}\frac{\cos\theta}{1-\cos\theta}, \quad y = \frac{1}{2}\frac{\sin\theta}{1-\cos\theta} \ \cdots [A]
\]という関係が手にはいる。この部分で使うのはオイラーの公式で得られる次の有名な恒等式である。
\[
\cos\theta = \frac{e^{i\theta}+e^{-i\theta}}{2}, \quad \sin\theta = \frac{e^{i\theta}-e^{-i\theta}}{2i}
\]
また、上の結果を使って得られる、次の計算結果も役にたつ。
\[
(e^{i\theta}-1) (e^{-i\theta}-1) = 2(1-\cos\theta)
\]
xとcosθの関係式を逆に解いて、cosθをxで表すと\(\cos\theta = -\frac{2x}{1-2x}\)となる。この結果を用いて、次にyとsinθの関係を計算することができる。結果は\(y=-\frac{2x-1}{2}\sin\theta\)である。\(\cos^2\theta+\sin^2\theta=1\)の関係式を用いるとθを消去することができて、
\[
\frac{4x^2}{(2x-1)^2} + \frac{4y^2}{(2x-1)^2} = 1
\]となる。これを整理すると
\[
x=-y^2 + \frac{1}{4}
\]を得る。つまり、軌跡はx軸方向に倒れた放物線である。
さて、問題となるのは、答えとなる軌跡Rはこの放物線全体ではないという点である。PはC’の上を動くだけであるので、θの範囲を\(\frac{\pi}{3}\le \theta \le \frac{5\pi}{3}\)に限らなければならない。
ちなみに、5つ上の式(式[A])を用いてgnuplotでパラメータ表示すると、下の図のようになる(これが答えである)。
式[A]を見ると、xはcosθのみで表されているから偶関数である。θの定義域の対称性と、θの関数としてのxの対称性を考えれば、θ=πのときにx=1/4となって放物線の頂点に対応することがわかる。したがって、θ=π/3, 5π/3の時にx=-1/2となり、ここがxの最小値である。つまり、xの範囲は\(-\frac{1}{2}\le x \le \frac{1}{4}\)である。一方、式[A]をみるとyは奇関数であり、対応するyの値は\(y=\pm\sqrt{3}/2\)である。
オイラーの公式を使うと(代数の計算はちょっと面倒になるが)、この手の問題は簡単に解くことができた。個人的には、この問題は「難」どころか「易」に感じる。というのも、上の解答をみたらわかるように、これは三角関数を含む代数計算の練習問題に過ぎない。
オイラーの公式と回転行列で解く:東大2018問5
2018年の東大2次試験が終わった。河合塾の分析によると「やや難化」だそうである。特に難しかったのが問5の複素数の問題だったという評価である。
ということで、さっそく5番から解いて見たいと思う。
最初に、この問題で採用されている記号の意味を明らかにしておこう。例えば、P(z)という表現だが、これは「点Pは複素数zによって表される」という意味になるらしい。A(1)は、「点Aすなわちz=1」ということである。ベクトル風に書けば、z=x+iyとしたとき、P(z)=P(x,y), A(1)=A(1,0)ということになる。
次に、\(z\)の複素共役を\(\bar{z}\)ではなく、\(z^*\)で表すことにする。前者は高校数学では採用されているらしいが、物理では世界的に後者を採用している。
(1)をオイラーの公式と代数幾何で解いてみよう。円C上の点Pはベクトル風に書けば\((\cos\theta,\sin\theta)\)となる。この問題では\(0\le\theta<2\pi\)という範囲を考えれば十分である。オイラーの公式を使ってまとめると\(z=\exp(i\theta)=\cos\theta + i\sin\theta\)となる。\(\theta \ne 0\)の時、点Pにおける接線の一般的な方程式をまとめると「やや」複雑な式となる。これを計算するのは不可能ではないが、面倒な計算を扱うはめになる。これを避けるには、座標系を回転させればよい。
まずは円の中心(つまり原点)の周りに、時計回りの方向に点Pを回転させx軸に重ねる。2次元のデカルト座標において回転行列は次のように定義される。
\[R(\theta)=\left(\begin{array}{cc}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{array}\right).\]ただし、回転の方向は、反時計回りが正の方向(+θ)として定義される。つまり\(R(-\theta)P(z)=P'(z')=P'(1)\)である。
回転後の座標系では、接線はx=1で表される垂直な直線である。一方、点Aは回転によって
\[R(-\theta)A(1)=A'(z^*)\]と変換される。ただし、\(z^* = \exp(-i\theta)=\cos\theta - i\sin\theta\)である。したがって、この垂線に関して「線対称」な点\(Q'(u')\)はベクトル風に考えれば簡単にわかる。ここで、\(u'=x_u'+iy_u'\)と表すことにしよう。点A'から垂線までの距離は\(1-\cos\theta\)である。よって、\(x_u' = 1 + (1-\cos\theta)\)である。一方、y座標のほうは変化がないので\(y_u'=-\sin\theta\)となる。
回転後の座標は自分に都合の良い座標にしてあるので、問題で与えられた座標に戻ることにする。もとに戻るには\(R(\theta)\)を作用させればよい。
\[
Q(u) = R(\theta)Q'(u') =R(\theta)\left(\begin{array}{c}x_u'\\ y_u'\end{array}\right) =\left(\begin{array}{c}2\cos\theta + \sin^2\theta - \cos^2\theta\\ 2\sin\theta-2\sin\theta\cos\theta\end{array}\right)
\]
加法定理(倍角の定理?)を使って整理すると、\(\sin^2\theta - \cos^2\theta = -\cos(2\theta), 2\cos\theta\sin\theta=\sin(2\theta)\)なので、
\[
Q(u): u = 2\left(\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right) -\left(\begin{array}{c}\cos(2\theta)\\ \sin(2\theta)\end{array}\right) =2z-z^2
\]となる。第二項は\(z^2 = (\exp(i\theta))^2 = (e^{i\theta})^2 = e^{2i\theta} =\cos(2\theta)+i\sin(2\theta)\)により正当化される。
\(w^*/w\)の値は、上の値を代入して複素数の代数を丁寧に計算すればすぐに
\[
\frac{w^*}{w} = \frac{1-u}{1-u^*} = \frac{(z-1)^2}{(z^*-1)^2} = \left(\frac{z-1}{z^{-1}-1}\right)^2 = z^2
\]
となることがわかる。ただし、\(z^* = (e^{i\theta})^* = e^{-i\theta} = 1/z\)という性質を最後に使った。
最後の計算も、これまでの計算の結果を使えば、簡単な代数計算に過ぎない。ただし、\(|z|/|w|=|z/w|\)という性質を覚えておく必要がある(といっても、忘れた時は、オイラーの公式を使ってすぐに確認できる)。
\[
\frac{\left|w+w^*-1\right|}{\left|w\right|} = \left|\frac{w+w^*-1}{w}\right|
=\left|(1-\frac{1}{w}) + \frac{w^*}{w}\right| = \cdots = 2|z| = 2
\]となる。zは円Cの周上にあるからその絶対値は1である。
これで(1)は終わりである。オイラーの公式と代数幾何(ベクトル)を組み合わせることで、簡単な複素数の代数計算にreduceすることができた。
ということで、さっそく5番から解いて見たいと思う。
問題5:複素平面上の原点を中心とする半径1の円をCとする。点\(P(z)\)はC上にあり,点A(1)とは異なるとする。点Pにおける円Cの接線に関して, 点Aと対称な点を\(Q(u)\)とする。\(\displaystyle w=\frac{1}{1-u}\)とおき,\(w\)と共役な複素数を\(\bar{w}\)で表す。
(1) \(u\)と\(\displaystyle \frac{\bar{w}}{w}\)を\(z\)についての整式として表し,絶対値の商\(\displaystyle\frac{\left|w+\bar{w}-1\right|}{\left|w\right|}\)を求めよ。複素数の問題を解く方針として、「複素数の問題は幾何学で解く」という方針を昨年掲げた。今年もこれでいってみよう。
最初に、この問題で採用されている記号の意味を明らかにしておこう。例えば、P(z)という表現だが、これは「点Pは複素数zによって表される」という意味になるらしい。A(1)は、「点Aすなわちz=1」ということである。ベクトル風に書けば、z=x+iyとしたとき、P(z)=P(x,y), A(1)=A(1,0)ということになる。
次に、\(z\)の複素共役を\(\bar{z}\)ではなく、\(z^*\)で表すことにする。前者は高校数学では採用されているらしいが、物理では世界的に後者を採用している。
(1)をオイラーの公式と代数幾何で解いてみよう。円C上の点Pはベクトル風に書けば\((\cos\theta,\sin\theta)\)となる。この問題では\(0\le\theta<2\pi\)という範囲を考えれば十分である。オイラーの公式を使ってまとめると\(z=\exp(i\theta)=\cos\theta + i\sin\theta\)となる。\(\theta \ne 0\)の時、点Pにおける接線の一般的な方程式をまとめると「やや」複雑な式となる。これを計算するのは不可能ではないが、面倒な計算を扱うはめになる。これを避けるには、座標系を回転させればよい。
まずは円の中心(つまり原点)の周りに、時計回りの方向に点Pを回転させx軸に重ねる。2次元のデカルト座標において回転行列は次のように定義される。
\[R(\theta)=\left(\begin{array}{cc}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{array}\right).\]ただし、回転の方向は、反時計回りが正の方向(+θ)として定義される。つまり\(R(-\theta)P(z)=P'(z')=P'(1)\)である。
回転後の座標系では、接線はx=1で表される垂直な直線である。一方、点Aは回転によって
\[R(-\theta)A(1)=A'(z^*)\]と変換される。ただし、\(z^* = \exp(-i\theta)=\cos\theta - i\sin\theta\)である。したがって、この垂線に関して「線対称」な点\(Q'(u')\)はベクトル風に考えれば簡単にわかる。ここで、\(u'=x_u'+iy_u'\)と表すことにしよう。点A'から垂線までの距離は\(1-\cos\theta\)である。よって、\(x_u' = 1 + (1-\cos\theta)\)である。一方、y座標のほうは変化がないので\(y_u'=-\sin\theta\)となる。
回転後の座標は自分に都合の良い座標にしてあるので、問題で与えられた座標に戻ることにする。もとに戻るには\(R(\theta)\)を作用させればよい。
\[
Q(u) = R(\theta)Q'(u') =R(\theta)\left(\begin{array}{c}x_u'\\ y_u'\end{array}\right) =\left(\begin{array}{c}2\cos\theta + \sin^2\theta - \cos^2\theta\\ 2\sin\theta-2\sin\theta\cos\theta\end{array}\right)
\]
加法定理(倍角の定理?)を使って整理すると、\(\sin^2\theta - \cos^2\theta = -\cos(2\theta), 2\cos\theta\sin\theta=\sin(2\theta)\)なので、
\[
Q(u): u = 2\left(\begin{array}{c}\cos\theta\\ \sin\theta\end{array}\right) -\left(\begin{array}{c}\cos(2\theta)\\ \sin(2\theta)\end{array}\right) =2z-z^2
\]となる。第二項は\(z^2 = (\exp(i\theta))^2 = (e^{i\theta})^2 = e^{2i\theta} =\cos(2\theta)+i\sin(2\theta)\)により正当化される。
\(w^*/w\)の値は、上の値を代入して複素数の代数を丁寧に計算すればすぐに
\[
\frac{w^*}{w} = \frac{1-u}{1-u^*} = \frac{(z-1)^2}{(z^*-1)^2} = \left(\frac{z-1}{z^{-1}-1}\right)^2 = z^2
\]
となることがわかる。ただし、\(z^* = (e^{i\theta})^* = e^{-i\theta} = 1/z\)という性質を最後に使った。
最後の計算も、これまでの計算の結果を使えば、簡単な代数計算に過ぎない。ただし、\(|z|/|w|=|z/w|\)という性質を覚えておく必要がある(といっても、忘れた時は、オイラーの公式を使ってすぐに確認できる)。
\[
\frac{\left|w+w^*-1\right|}{\left|w\right|} = \left|\frac{w+w^*-1}{w}\right|
=\left|(1-\frac{1}{w}) + \frac{w^*}{w}\right| = \cdots = 2|z| = 2
\]となる。zは円Cの周上にあるからその絶対値は1である。
これで(1)は終わりである。オイラーの公式と代数幾何(ベクトル)を組み合わせることで、簡単な複素数の代数計算にreduceすることができた。
2018年2月2日金曜日
センター試験の数学II:第4問(代数方程式の性質)
3次方程式の一般解の個数は3つになるが、そのうち一つが虚数、そのうち一つが実数である特別な場合の「研究」が、第4問のテーマである。
一般にn次方程式の解の個数はn個ある。その内の一つが複素数解\(z_0\)であるならば、その複素共役\(z_0^*\)も解となる。これは簡単に証明できる。例えば、此の問題のような3次方程式\[ z^3+az^2+bz+c=0\]が与えられているとする。複素数\(z_0\)が解ならば、当然\(z_0^3+az_0^2+bz_0+c=0\)は成立する。この式の複素共役を取ると\((z_0^*)^3+a(z_0^*)^2+bz_0^*+c=0\)であるから、\(z=z_0^*\)もこの3次方程式の解である。この証明では、a,b,cは実数であることを利用するのが重要である。
問題では、\(z=-1+\sqrt{6}i\)が解だと与えられているので、上の考察から\(z=-1-\sqrt{6}i\)も解であることがわかる。したがって、与式は\((x-x_0)(x+1-\sqrt{6}i) (x+1+\sqrt{6}i)=0\)と因数分解できる。すなわち、\(x^3+ax^2+bx+c=(x-x_0)(x^2+2x+7)\)ということである。xの次数ごとに係数を比較すると、\(a=-x_0+2, b=-2x_0+7, c=-7x_0\)となる。最初の式から\[x_0=-a+2,\]これをbとcの式に代入すると、\[ b=2a+3, \quad c=7a-14\]を得る。
さて、試験問題を解く、という観点からすると、アイ、ウエ、オカ、キに関しては、実部と虚部それぞれが0になる、という条件から計算すればよい。試験問題で途中まで形が暴露されているので、これを利用しよう。実部は\(\alpha a - b + c + \beta\)という形になるそうだから、上の結果を用いてaの一次式で表すと、\[\alpha a -2a-3+7a-14+\beta = (\alpha + 5) +\beta-17 =0\]なので、\(\alpha = -5, \beta=17\)と計算できる。虚部に関してもまったく同様の計算をすればよい。
\(P(x)=(x+a-2)(x^2+2x+7)\)を\(x^2+2x+7\)で割ったときの、商はx+a-2であることは明らかで、と余りも自明の値(0)となる。これで、ここまでの「問題」は全て解くことができた。
最後の部分は剰余定理である。\(P(x)= (x+a-3)f(x) + 6\)である、と問題文で言っているので(ただしf(x)は2次式)、P(-a+3)を計算し、それが6になることを利用してaを決めればよい。\(P(-a+3) = (-a+3+a-2)((-a+3)(-a+3+2)+7) = (-a+3)(-a+5)+7 \\ = a^2-8a+15+7 =a^2-8a+22\)である。したがって、\(a^2-8a+16=0\)という2次式の解が求めるaである。これを解くと、\(a=4\)であることがわかる。
この値のとき\(P(x)=(x+2)(x^2+2x+7)\)となるので、\(P(x) = (x^2+px+q)(x-1) + 13x+17\)と係数を比較するとpとqが求まる。
こういうタイプの、係数を比較する計算は、物理実験や物理シミュレーションのデータ処理や数値分析でよく利用される。理論物理でもよくやるので(特に現象論では)よく習熟しておく必要があるだろう。
第3問も面白そうな問題ではあるが、センター試験の問題を解くのもそろそろ飽きてきたのでスキップすることにしよう。今年は、MathJaXのおかげで、ずいぶん仕事がはかどった。センター試験の問題を6問も解くことができた。「十分に準備運動できた」とみなし、この辺でセンター試験をみるのはやめにして、二次試験を待つこととしよう。
昨年から今年にかけて、阪大と京大の物理の入試問題で不備が見つかり、大きな問題となった。どちらも音波/ドップラー効果の問題であった。原因はいろいろあると思うが、高校物理の教え方に大きな問題があると思っている。
日本の大学で力学や電磁気学、熱力学などを教えていて感じるのは、多くの学生が大学の物理を習う時に大きな困惑を示し、その主因が「大学の物理は「物理」ではなく、数学だ」と考えていることである。この感覚は非常に問題だ。
物理の「言語」は数学なので、物理を議論するには「数学を喋る」必要がある。数学といっても、現代数学が扱うような数学ではなく、すでに確立した「古い」数学である。
たとえば、高校生が英語を学ぶ目的は、「英語学」を習得することではない。将来、経済学や文学や歴史を世界の人びとと語り合うときに、共通言語で議論する必要があるから「英語」を学ぶのである。同様に、世界中の物理学者と議論するときには、「共通言語」である数学を利用するのが現代の物理学なのである。
にもかかわらず、日本の高校では数学をなるべく使わないように指導する。微分積分を基礎とする力学や、三角関数やフーリエ理論を基本にする波動、偏微分や多変数解析を用いる熱力学などにおいて、その数学的手法の多くを犠牲にして、無理な形で「高校物理」を教えている。物理の「基礎」である数学を取り除いた「高校物理」は、物理学者にとっては非常にとっつきにくいものであり、強い違和感を感じる。それが故に、高校物理の問題はあまり興味を持てずに、このブログでは高校数学ばかりを解いているのである。
自分がもし「高校物理を使った試験問題を作れ」と要請されたら、非常に困惑するだろうと思う。大学の物理関係者が「高校物理が苦手」なのは、阪大や京大に限らず、実は普遍的なのではないだろうか?だとすると、高校物理という分野自体を「物理」とは思わずに、独特の学問分野として研究し、それを「本当の物理」とどう関連づけていくかという問題は、これから重要になってくるのかもしれない。これからは、高校物理にも興味をもってあたっていこうかな、と感じている次第である。
一般にn次方程式の解の個数はn個ある。その内の一つが複素数解\(z_0\)であるならば、その複素共役\(z_0^*\)も解となる。これは簡単に証明できる。例えば、此の問題のような3次方程式\[ z^3+az^2+bz+c=0\]が与えられているとする。複素数\(z_0\)が解ならば、当然\(z_0^3+az_0^2+bz_0+c=0\)は成立する。この式の複素共役を取ると\((z_0^*)^3+a(z_0^*)^2+bz_0^*+c=0\)であるから、\(z=z_0^*\)もこの3次方程式の解である。この証明では、a,b,cは実数であることを利用するのが重要である。
問題では、\(z=-1+\sqrt{6}i\)が解だと与えられているので、上の考察から\(z=-1-\sqrt{6}i\)も解であることがわかる。したがって、与式は\((x-x_0)(x+1-\sqrt{6}i) (x+1+\sqrt{6}i)=0\)と因数分解できる。すなわち、\(x^3+ax^2+bx+c=(x-x_0)(x^2+2x+7)\)ということである。xの次数ごとに係数を比較すると、\(a=-x_0+2, b=-2x_0+7, c=-7x_0\)となる。最初の式から\[x_0=-a+2,\]これをbとcの式に代入すると、\[ b=2a+3, \quad c=7a-14\]を得る。
さて、試験問題を解く、という観点からすると、アイ、ウエ、オカ、キに関しては、実部と虚部それぞれが0になる、という条件から計算すればよい。試験問題で途中まで形が暴露されているので、これを利用しよう。実部は\(\alpha a - b + c + \beta\)という形になるそうだから、上の結果を用いてaの一次式で表すと、\[\alpha a -2a-3+7a-14+\beta = (\alpha + 5) +\beta-17 =0\]なので、\(\alpha = -5, \beta=17\)と計算できる。虚部に関してもまったく同様の計算をすればよい。
\(P(x)=(x+a-2)(x^2+2x+7)\)を\(x^2+2x+7\)で割ったときの、商はx+a-2であることは明らかで、と余りも自明の値(0)となる。これで、ここまでの「問題」は全て解くことができた。
最後の部分は剰余定理である。\(P(x)= (x+a-3)f(x) + 6\)である、と問題文で言っているので(ただしf(x)は2次式)、P(-a+3)を計算し、それが6になることを利用してaを決めればよい。\(P(-a+3) = (-a+3+a-2)((-a+3)(-a+3+2)+7) = (-a+3)(-a+5)+7 \\ = a^2-8a+15+7 =a^2-8a+22\)である。したがって、\(a^2-8a+16=0\)という2次式の解が求めるaである。これを解くと、\(a=4\)であることがわかる。
この値のとき\(P(x)=(x+2)(x^2+2x+7)\)となるので、\(P(x) = (x^2+px+q)(x-1) + 13x+17\)と係数を比較するとpとqが求まる。
こういうタイプの、係数を比較する計算は、物理実験や物理シミュレーションのデータ処理や数値分析でよく利用される。理論物理でもよくやるので(特に現象論では)よく習熟しておく必要があるだろう。
第3問も面白そうな問題ではあるが、センター試験の問題を解くのもそろそろ飽きてきたのでスキップすることにしよう。今年は、MathJaXのおかげで、ずいぶん仕事がはかどった。センター試験の問題を6問も解くことができた。「十分に準備運動できた」とみなし、この辺でセンター試験をみるのはやめにして、二次試験を待つこととしよう。
昨年から今年にかけて、阪大と京大の物理の入試問題で不備が見つかり、大きな問題となった。どちらも音波/ドップラー効果の問題であった。原因はいろいろあると思うが、高校物理の教え方に大きな問題があると思っている。
日本の大学で力学や電磁気学、熱力学などを教えていて感じるのは、多くの学生が大学の物理を習う時に大きな困惑を示し、その主因が「大学の物理は「物理」ではなく、数学だ」と考えていることである。この感覚は非常に問題だ。
物理の「言語」は数学なので、物理を議論するには「数学を喋る」必要がある。数学といっても、現代数学が扱うような数学ではなく、すでに確立した「古い」数学である。
たとえば、高校生が英語を学ぶ目的は、「英語学」を習得することではない。将来、経済学や文学や歴史を世界の人びとと語り合うときに、共通言語で議論する必要があるから「英語」を学ぶのである。同様に、世界中の物理学者と議論するときには、「共通言語」である数学を利用するのが現代の物理学なのである。
にもかかわらず、日本の高校では数学をなるべく使わないように指導する。微分積分を基礎とする力学や、三角関数やフーリエ理論を基本にする波動、偏微分や多変数解析を用いる熱力学などにおいて、その数学的手法の多くを犠牲にして、無理な形で「高校物理」を教えている。物理の「基礎」である数学を取り除いた「高校物理」は、物理学者にとっては非常にとっつきにくいものであり、強い違和感を感じる。それが故に、高校物理の問題はあまり興味を持てずに、このブログでは高校数学ばかりを解いているのである。
自分がもし「高校物理を使った試験問題を作れ」と要請されたら、非常に困惑するだろうと思う。大学の物理関係者が「高校物理が苦手」なのは、阪大や京大に限らず、実は普遍的なのではないだろうか?だとすると、高校物理という分野自体を「物理」とは思わずに、独特の学問分野として研究し、それを「本当の物理」とどう関連づけていくかという問題は、これから重要になってくるのかもしれない。これからは、高校物理にも興味をもってあたっていこうかな、と感じている次第である。
2018年2月1日木曜日
センター試験の数学IIB2018:第4問(重心の性質の拡張)
数II・Bの問題にはあまり面白い問題はなかったが、第4問だけは1次独立の概念の練習になるだろうと思って取り上げることに決めた。
下の図は、a=3/5とし、\(\angle ABC = 60^\circ\)とおいてpostscriptで作図したものである。BCの長さは4とした。これらの仮定によりA(-4,0), B(0,0), C(-2,-2√3)が決まる。ちなみに、問題文では\(AD:BD=1:3, BE:CE=a:1-a\)と与えられているだけであるが、上の仮定を用いると、D(-3,0), E(-6/5, 6√3/5)であることも決まる。Fの座標も計算できるだろが、ここではCDとAEの交点として表すにとどめておく。
三角形が成立している時点で、任意の二辺を選び、その方向にベクトルを設定すれば、それらは1次独立なベクトルになっていることは保証される。したたって、これら2つの1次独立なベクトルをこの平面の基底ベクトルに選べば、平面にある任意のベクトルは、この基底の線形結合で表すことができる。一般にn次元(ベクトル)空間における、1次独立な基底の最大数はnであり、そのn個の基底の組のことを完全系という。これは線形代数の基本であり、量子力学やその他の物理学で重要な役割を果たす概念である。この問題では、完全系に選ぶべき基底の候補として\(\mathbf{p}=\vec{FA}, \mathbf{q}=\vec{FB}, \mathbf{r}=\vec{FC}\)を提案している。ちなみに、大学の物理ではベクトルを太字で表すので、ここでもそれを採用した。完全系を作るには2つで十分なので、どれか一つは余分(redundant)である。つまり、3つのうち、2つは独立に取れるが、最後の1つは独立な2つの基底の線形結合で書けることになる。この問題では、この性質を(暗に)使って解かせている。
この問題でもう一つ大事な点は、内分点の表現である。例えば、問題では\(\vec{FD}\)を\(\mathbf{p}\)と\(\mathbf{q}\)の線形結合で表せ、という問があるが、これは直線ABを1:3に内分する点Dに(点Fから)向かうベクトルに相当する。
問題を一般化して、AD:BD=m:nの場合、FDはどのように表現できるか調べてみる。
\[\vec{FD}=\vec{FA}+\vec{AD}\]である。右辺を\(\mathbf{p}\)と\(\mathbf{q}\)で書き直すのが目標である。右辺第一項は定義により\(\mathbf{p}\)である。第二項は、\[\vec{AB}=\vec{FB}-\vec{FA} = \mathbf{q}-\mathbf{p}\]を用いて、\(\vec{AD} = \frac{m}{m+n}\vec{AB}\)と表すことができる。これを代入すると、
\[\vec{FD}=\frac{n}{m+n}\mathbf{p} + \frac{m}{m+n}\mathbf{q}\]を得る。まとめると、始点を共有する2つの(1次独立な)ベクトル\(\mathbf{p},\mathbf{q}\)が成す三角形を考える時、ベクトルの始点の先にある「斜辺」の内分点に、(始点から)向かう「内分ベクトル」は上の公式で表せる、ということだ。
\(\vec{FD}\)は\(\mathbf{r}\)に平行(1次従属)なので、\[\vec{FD}=s\mathbf{r}\]と書いてもよい。ただし、sは負の実数。この関係と上の内分点公式から、\(\mathbf{r}\)を\(\mathbf{p}\)と\(\mathbf{q}\)の線形結合表現を手にいれることができることを示している点が、この問題の面白いところである。すなわち、
\[\mathbf{r}=\frac{1}{s(m+n)}\left(n\mathbf{p} + m\mathbf{q}\right)\]
この関係式は一意的(英語ではuniqueという)なので、pとqの線形結合でrを表す別の表現というものは存在しないのである。この性質を用いて、今度は(\vec{FE}\)に関して同じように考え、pをrとqの線形結合で表してみる。BE:CE=a:1-aなので、今度は
\[\mathbf{p} = \frac{1}{t}\left((1-a)\mathbf{q}+a\mathbf{r}\right)\]という関係式を得る。ただし、tは負の実数で、\(\vec{FE}=t\mathbf{p}\)という形で定義する。上式をrについて解き直すと、\[\mathbf{r}=\frac{t}{a}\mathbf{p} -\frac{1-a}{a}\mathbf{q}\]
である。先に求めたrの関係式と、今求めたrの関係式は「等価」でなくてはならない、というのがベクトル空間の性質であるから、係数の間に関係式が発生し、sとtが定まる。
\[s=\frac{m}{m+n}\frac{a}{1-a}, t = \frac{n}{m}(1-a)\]
これにより、線分CDは、点Fによって、CF:DF=1:sに内分されていることや、線分AEは点Fによって、AF:EF=1:tに内分されていることもわかってしまう。
応用問題として、m=n, a=1/2の場合を考えてみよう。これはAからBCの中点Eに直線(AE)を引き、Cから直線(AB)の中点Dへ直線(CD)を下ろした状況に一致する。直線AEとCDの交点Fはいわゆる「重心」である。重心Fによって直線AEやCDは、2:1に分割されることが知られているが、それを確認してみよう。\(s=\frac{m}{2m}\frac{1/2}{1-1/2} =\frac{1}{2}, t=\frac{1}{2}\)であるから、CF:DF=AF:EF=1:1/2=2:1となり、確認ができた。
此の問題は、おそらく重心の性質を一般化することから思いついたものであろう。三角形の2つの辺をm:n,およびa:1-aに分割する頂点からの直線同士の交点が、その直線を1:sや1:tに分割するという「新しい」性質を解明したことに相当する。
2018年1月31日水曜日
センター試験の数学2018:第5問(幾何はすべて代数幾何で解く)
公式や定理をたくさん覚え、それをどう使いこなすかというのが幾何の解き方だとすると、定理を忘れてしまうとどうにも手が出せない。余弦定理、正弦定理、メネラウスの定理、チェバの定理、いろいろある。今回のセンター試験の問題5では「角の二等分線の定理」とやらを使う問題が出た。しかし、そんな「マイナーな定理」を忘れてしまった人はどうすればよいのだろうか?
私の方針は以前より首尾一貫している。デカルトの編み出した代数幾何である。 幾何の問題を代数の問題に書き直すのである。こうすれば、定理を忘れた時には、連立方程式や判別式の計算をするだけで答えが手にはいる。
代数幾何学でもっとも重要なのは、どのような座標系を選ぶかである。うまい座標系を選べばあっという間に解にたどり着ける問題でも、まずい座標系で解き始めると本当に苦労することがある。これは物理学でも同じことで、最初に選んだ座標系では手も出せないような多体問題が、カノニカル変換によって座標変換するとあっという間に解けてしまったりする。超電導のBCS理論で出てくるボゴリウボフ変換がそのよい例だ。「実粒子」ではなく、見方を変えて「準粒子」を用いて問題を解いた方が見通しがよくなるのである。
さて、センター試験の第5問では直角三角形が出てくる。2次元のデカルト座標系 は直交座標だから、原点に点Aを合わせ、線分ABがx軸に、線分ACがy軸になるように選ぶと自然な座標系の選び方となる。
次に、点A(原点)を通り、直線BCに接するような円を考え、この円とABの交点のうち、Aでない点をEとする。したがって、O=A(0,0), B=(2,0), C=(0,1)となる。問題ではいきなりBDの長さを計算させているが、ここではあえて、円の方程式を求めた後、連立方程式を用いてDとEの座標を計算してみよう。まず円の方程式を\[ (x-p)^2 + (y-q)^2 = r^2\]とおく。この円は原点を通るので\[p^2 + q^2 = r^2\]であることがまず示せる。したがって、円の方程式は\[x^2 -2px + y^2 - 2qy = 0\]となる。次に、直線BCの方程式は\[y= -\frac{1}{2}x + 1\]であることはすぐにわかる。この直線と円は接するというので、連立方程式から得られる二次方程式の判別式が0とならねばならない。yを消去して、xについての2次式を計算すると、\[5x^2 - 4(2p-q+1)x+4(1-2q)=0\]を得る。判別式が0となるので\[ \{2(2p-q+1)\}^2 - 5\cdot 4(1-2q) = 0\]である。最後に、この接点は点Dに他ならず、それは直線BCと直線ADの交点である。直線ADの方程式は\[y=x\]に他ならない(直角の2等分線だから)。したがって、連立方程式を解くことで、ADとBCの交点の座標Dが求まり、それはD(2/3,2/3)となる。円の方程式にこの値を代入すると、\[p+q = \frac{2}{3}\]を得る。これを判別式=0の条件に代入してqを消去すると、pに関する二次式\[\left(3p-\frac{4}{3}\right)^2=0\]を得るが、この方程式の解は簡単に求まって\(p=\frac{4}{9}\)の重解である。また\(q=\frac{2}{9}\)であることも容易に計算できる。同様に、円の半径の自乗は\(r^2 = p^2 + q^2 =\frac{20}{81}\)と計算される。以上より、円の方程式は\[\left(x-\frac{4}{9}\right)^2 + \left(y-\frac{2}{9}\right)^2 = \frac{20}{81}\]である。
点Eの座標は円がx軸と交わる場所であるから、上の方程式にy=0を代入し、xについての方程式\[\left(x-\frac{4}{9}\right)^2 + \frac{4}{81} = \frac{20}{81}\]を解けばよい。この方程式の解は\(x=0, \frac{8}{9}\)となるが、最初の解は点Aに相当するので、2つ目の解を選ぶ。つまり\(E(\frac{8}{9},0)\)である。
点A,B,C,D,Eのすべての座標がわかってしまったので、あとはピタゴラスの定理を駆使して2点間の距離を計算するだけで、線分の長さはすべて手にはいる!これが「代数」幾何の強みに他ならない。(もちろん、幾何の定理を知っていれば試験中にもっと早く計算できるかもしれない。しかし、その定理を覚えるためには勉強時間を長くしなくてはならないし、万が一忘れてしまったらその勉強時間は無駄になってしまう。)
ではいつものように、以上で得た情報を元にpostscriptで作図してみよう。
つづく問題では、直線EDの表す方程式のy切片(点F)に相当する値が必要となる。点Fの座標を求めておこう。点EとDを通る直線の方程式は\[ y = \frac{2/3}{2/3-8/9}(x-8/9)=-3x+\frac{8}{3}\]である。したがって、\(F(0,\frac{8}{3})\)となる。
最後の問題は、重心、外心、内心の3種類の点の定義を覚えているかどうか、というある意味「つまらない質問」である。が、これも代数幾何でなんとか突破できると思う。答えは内心であるが、それは\(\angle ABC = \angle FBC\)を示すことで証明できる。
ちなみに、重心や外心ならば、AC=FCとなっているはずだが、明らかにそれは成り立っていない。さらに外心ならばAC=FCであるのみならず、CBはx軸に平行な直線であるべきだが、あきらかに傾きを持っている。重心と外心はしたがって候補から簡単に外れる。消去法で答えは内心となるのだが、これでは「問題が解ける」だけであって、数学の研究とはならない。積極的な方法(active approach)で内心であることを示そう。
方法はいろいろあるが、一つの方法としては\[\tan\angle ABF = \frac{2\tan\angle ABC}{1-\tan^2\angle ABC}\]を確認することである。これは簡単に確認できる。
ちなみに、この内心を中心とする内接円は\[(x-\frac{2}{3})^2+(y-\frac{2}{3})^2 = (\frac{2}{3})^2\]で表される。
私の方針は以前より首尾一貫している。デカルトの編み出した代数幾何である。 幾何の問題を代数の問題に書き直すのである。こうすれば、定理を忘れた時には、連立方程式や判別式の計算をするだけで答えが手にはいる。
代数幾何学でもっとも重要なのは、どのような座標系を選ぶかである。うまい座標系を選べばあっという間に解にたどり着ける問題でも、まずい座標系で解き始めると本当に苦労することがある。これは物理学でも同じことで、最初に選んだ座標系では手も出せないような多体問題が、カノニカル変換によって座標変換するとあっという間に解けてしまったりする。超電導のBCS理論で出てくるボゴリウボフ変換がそのよい例だ。「実粒子」ではなく、見方を変えて「準粒子」を用いて問題を解いた方が見通しがよくなるのである。
さて、センター試験の第5問では直角三角形が出てくる。2次元のデカルト座標系 は直交座標だから、原点に点Aを合わせ、線分ABがx軸に、線分ACがy軸になるように選ぶと自然な座標系の選び方となる。
次に、点A(原点)を通り、直線BCに接するような円を考え、この円とABの交点のうち、Aでない点をEとする。したがって、O=A(0,0), B=(2,0), C=(0,1)となる。問題ではいきなりBDの長さを計算させているが、ここではあえて、円の方程式を求めた後、連立方程式を用いてDとEの座標を計算してみよう。まず円の方程式を\[ (x-p)^2 + (y-q)^2 = r^2\]とおく。この円は原点を通るので\[p^2 + q^2 = r^2\]であることがまず示せる。したがって、円の方程式は\[x^2 -2px + y^2 - 2qy = 0\]となる。次に、直線BCの方程式は\[y= -\frac{1}{2}x + 1\]であることはすぐにわかる。この直線と円は接するというので、連立方程式から得られる二次方程式の判別式が0とならねばならない。yを消去して、xについての2次式を計算すると、\[5x^2 - 4(2p-q+1)x+4(1-2q)=0\]を得る。判別式が0となるので\[ \{2(2p-q+1)\}^2 - 5\cdot 4(1-2q) = 0\]である。最後に、この接点は点Dに他ならず、それは直線BCと直線ADの交点である。直線ADの方程式は\[y=x\]に他ならない(直角の2等分線だから)。したがって、連立方程式を解くことで、ADとBCの交点の座標Dが求まり、それはD(2/3,2/3)となる。円の方程式にこの値を代入すると、\[p+q = \frac{2}{3}\]を得る。これを判別式=0の条件に代入してqを消去すると、pに関する二次式\[\left(3p-\frac{4}{3}\right)^2=0\]を得るが、この方程式の解は簡単に求まって\(p=\frac{4}{9}\)の重解である。また\(q=\frac{2}{9}\)であることも容易に計算できる。同様に、円の半径の自乗は\(r^2 = p^2 + q^2 =\frac{20}{81}\)と計算される。以上より、円の方程式は\[\left(x-\frac{4}{9}\right)^2 + \left(y-\frac{2}{9}\right)^2 = \frac{20}{81}\]である。
点Eの座標は円がx軸と交わる場所であるから、上の方程式にy=0を代入し、xについての方程式\[\left(x-\frac{4}{9}\right)^2 + \frac{4}{81} = \frac{20}{81}\]を解けばよい。この方程式の解は\(x=0, \frac{8}{9}\)となるが、最初の解は点Aに相当するので、2つ目の解を選ぶ。つまり\(E(\frac{8}{9},0)\)である。
点A,B,C,D,Eのすべての座標がわかってしまったので、あとはピタゴラスの定理を駆使して2点間の距離を計算するだけで、線分の長さはすべて手にはいる!これが「代数」幾何の強みに他ならない。(もちろん、幾何の定理を知っていれば試験中にもっと早く計算できるかもしれない。しかし、その定理を覚えるためには勉強時間を長くしなくてはならないし、万が一忘れてしまったらその勉強時間は無駄になってしまう。)
ではいつものように、以上で得た情報を元にpostscriptで作図してみよう。
最後の問題は、重心、外心、内心の3種類の点の定義を覚えているかどうか、というある意味「つまらない質問」である。が、これも代数幾何でなんとか突破できると思う。答えは内心であるが、それは\(\angle ABC = \angle FBC\)を示すことで証明できる。
ちなみに、重心や外心ならば、AC=FCとなっているはずだが、明らかにそれは成り立っていない。さらに外心ならばAC=FCであるのみならず、CBはx軸に平行な直線であるべきだが、あきらかに傾きを持っている。重心と外心はしたがって候補から簡単に外れる。消去法で答えは内心となるのだが、これでは「問題が解ける」だけであって、数学の研究とはならない。積極的な方法(active approach)で内心であることを示そう。
方法はいろいろあるが、一つの方法としては\[\tan\angle ABF = \frac{2\tan\angle ABC}{1-\tan^2\angle ABC}\]を確認することである。これは簡単に確認できる。
ちなみに、この内心を中心とする内接円は\[(x-\frac{2}{3})^2+(y-\frac{2}{3})^2 = (\frac{2}{3})^2\]で表される。
2018年1月30日火曜日
センター試験の数学2018:第4問
この整数問題は非常によい問題で、頭を動かして、手を動かして、その場で「考える」必要があるだろう。決まり切ったパターンで乗り切ろうとしてもなかなかうまくいかず、諦めてしまう人は多いと思うが、本来合格させたいと思う学生はこういう問題を解いてくる学生である。チャレンジした学生には「ボーナス点」を与えてもよいのではないだろうか?問題は3つのセクションに分かれていて、それぞれが独立の要素もありつつ、お互いに関連している。最初の部分でこけるとその後は全滅してしまうので、そこがこの問題の「問題点」かもしれない。
(1)素因数分解させた後に、因数分解(約数)の組み合わせの数を調べさせる問題。整数の問題と数え上げの問題が混じった、このタイプの問題を好きな人(出題者=大学の先生)は多いと思う。
今年のセンター試験では114が選ばれた。素因数分解は、\[114 = 2^4\cdot 3^2\]である。114の約数をすべて数え上げると幾つになるか?注意すべきは、1と114も約数に含まれるということ。
約数は\(2^m\cdot 3^n\)と表せる。ただし、\(m=0,1,2,3,4; n=0,1,2\)である。結局、約数の総数は、(m,n)の組み合わせ総数の数と同じである。 したがって、\(5\times 3=15\)が答えである。
(2) さきほど素因数分解した114が再び出てくる。今度は素数7との関わりを考えつつ、144と7が同時に関係する公倍数とか公約数について、一次式と絡めて解く良い問題である。与えられたのは\[144x-7y=1\]である。一見して一次関数のように見えるが、(x,y)は整数の組であることに注意を払う必要がある。つまり、このグラフは原子の一次元結晶のように点と点が離れて並んでいる「物体」であって、連続体としての「棒」が伸びているイメージを持ってはならない。
x,yについては負の整数となる可能性も考慮すべきだが、簡単な分析から不要であることがすぐにわかる。ただ、試験中にこの分析をしていると時間が取られてしまうし、その努力が評価もされないので、解答欄の大きさを見て(負の数なら符号の分の解答欄があるはず)正の整数と決めつけることになろう。ただ、こういう姿勢が染み付くと、大学に入ってから苦しむことになるので、本番以外では丁寧に分析して解く癖を身につけておくべきだ。ただ、問題には「xの絶対値が最小」という具合に、負の数を考えないように釘を刺している点には注意したい。まあ、受験上でこういう微妙な表現に気づくのは至難の技だとは思う。「試験慣れ」というのはこういうところであって、試験の点が高いことが学力の高さを意味するとは限らない、というのがよく出る場所だろう。(ボーアはこういう問題が得意だろうが、アインシュタインは苦手だろう。)
さて、|x|に着目するので |x|=0,1,2あたりを最初に当てはめて「実験的に」考えて見よう。このように「例題」を使って一般化を試みることは、数学者もよく使う方法だ。恥ずかしいことはひとつもない。まずx=0は当てはまらないことがすぐにわかる。つぎにx=1とx=-1を考えてみよう。x=-1の場合、\(7y=-144-1=-145=5\cdot 29\)であるから、整数解yは見つからない。29は素数である。x=1の場合は、\(7y = 144-1 =143 = 11\cdot 13\)となり、やはり7以外の素数同士の積が素数7の倍数となることはないので、これも場外される。x=-2がうまくいかないのは省略するとして、x=2の場合を試してみる。実はこれが正解になっている。\[ 7y = 144\cdot 2 -1 = 287 = 7\cdot 41\]
(x,y)=(2,41)が正解である。
次は、上の線形関係式を満たす一般の(x,y)の形を見つける問題だが、出題者の好意により\[x=mk+2, \quad y = nk + 41\]という形が与えられているから、これを最大限に利用しよう。k=0の場合が、上で求めた場合(x,y)=(2,41)に相当する。問題になっているのは整数m,nの値を決めることである。まずは、上の形は線形関係に代入する。定数部分の差が1となるのは(上の問題で)わかっているので、mとnが満たすべき関係として\(144m-7n=0\)を得る。因数分解の結果を用いると\[ n = \frac{2^4\cdot 3^2}{7}m\]となるが、nが整数となるためにはmは7の倍数である必要がある。よってm=7とおくと、n=144が自動的に決まる。(m=14とした場合は、k’=2kとくり込むことができる。)まとめると、\[ x=7k+2, \quad y=144k+41\]が 答えである。
(3)は(1)と(2)の結果を応用する問題であり、とても面白い問題だと思う。144の倍数というのは\(144k, \quad x=1,2,3,\cdots \)だから、\(2^4\cdot 3^2 k\)の構造を考えるとよい。(1)の結果として、144の約数の数は15個なので、kの部分をうまく選んで約数が18になるようにすればよい。しかし、問題文で「7で割ったら余りが1」でもある、という制限がつく。これは(2)の\(144x-7y=1\)を書き換えた\(144x = 7y+1\)と同じ意味である。つまり、\(k=1,2,3,\cdots\)と選ぶのではなく、144xに対して、\(x=7k+2, k=0,1,2,\cdots\)という具合に選んでいくのである。ここでも「実験」を行ってみる。k=0のときx=2であり、このとき\(144x = 2^5\cdot 3^2\)という構造を持つ。このときの約数の数は\(6\times 3 = 18\)となって題意に合致する。すなわち、\(144\times 2\)が「約数を18個持つ最小のもの」である。
同じような手順で、次は約数の数が30個のものを探す。k=1,2,3と試していくと、k=3のときその条件が満たされることが簡単に確認できる。このとき\(x=7\cdot 3 + 2 = 23\)であり、\(114\cdot 23 = 2^4\cdot 3^2 \cdot 23\)である。23は素数であるから、約数の数は\(5\times 3\times 2=30\)となるのである。
(1)素因数分解させた後に、因数分解(約数)の組み合わせの数を調べさせる問題。整数の問題と数え上げの問題が混じった、このタイプの問題を好きな人(出題者=大学の先生)は多いと思う。
今年のセンター試験では114が選ばれた。素因数分解は、\[114 = 2^4\cdot 3^2\]である。114の約数をすべて数え上げると幾つになるか?注意すべきは、1と114も約数に含まれるということ。
約数は\(2^m\cdot 3^n\)と表せる。ただし、\(m=0,1,2,3,4; n=0,1,2\)である。結局、約数の総数は、(m,n)の組み合わせ総数の数と同じである。 したがって、\(5\times 3=15\)が答えである。
(2) さきほど素因数分解した114が再び出てくる。今度は素数7との関わりを考えつつ、144と7が同時に関係する公倍数とか公約数について、一次式と絡めて解く良い問題である。与えられたのは\[144x-7y=1\]である。一見して一次関数のように見えるが、(x,y)は整数の組であることに注意を払う必要がある。つまり、このグラフは原子の一次元結晶のように点と点が離れて並んでいる「物体」であって、連続体としての「棒」が伸びているイメージを持ってはならない。
x,yについては負の整数となる可能性も考慮すべきだが、簡単な分析から不要であることがすぐにわかる。ただ、試験中にこの分析をしていると時間が取られてしまうし、その努力が評価もされないので、解答欄の大きさを見て(負の数なら符号の分の解答欄があるはず)正の整数と決めつけることになろう。ただ、こういう姿勢が染み付くと、大学に入ってから苦しむことになるので、本番以外では丁寧に分析して解く癖を身につけておくべきだ。ただ、問題には「xの絶対値が最小」という具合に、負の数を考えないように釘を刺している点には注意したい。まあ、受験上でこういう微妙な表現に気づくのは至難の技だとは思う。「試験慣れ」というのはこういうところであって、試験の点が高いことが学力の高さを意味するとは限らない、というのがよく出る場所だろう。(ボーアはこういう問題が得意だろうが、アインシュタインは苦手だろう。)
さて、|x|に着目するので |x|=0,1,2あたりを最初に当てはめて「実験的に」考えて見よう。このように「例題」を使って一般化を試みることは、数学者もよく使う方法だ。恥ずかしいことはひとつもない。まずx=0は当てはまらないことがすぐにわかる。つぎにx=1とx=-1を考えてみよう。x=-1の場合、\(7y=-144-1=-145=5\cdot 29\)であるから、整数解yは見つからない。29は素数である。x=1の場合は、\(7y = 144-1 =143 = 11\cdot 13\)となり、やはり7以外の素数同士の積が素数7の倍数となることはないので、これも場外される。x=-2がうまくいかないのは省略するとして、x=2の場合を試してみる。実はこれが正解になっている。\[ 7y = 144\cdot 2 -1 = 287 = 7\cdot 41\]
(x,y)=(2,41)が正解である。
次は、上の線形関係式を満たす一般の(x,y)の形を見つける問題だが、出題者の好意により\[x=mk+2, \quad y = nk + 41\]という形が与えられているから、これを最大限に利用しよう。k=0の場合が、上で求めた場合(x,y)=(2,41)に相当する。問題になっているのは整数m,nの値を決めることである。まずは、上の形は線形関係に代入する。定数部分の差が1となるのは(上の問題で)わかっているので、mとnが満たすべき関係として\(144m-7n=0\)を得る。因数分解の結果を用いると\[ n = \frac{2^4\cdot 3^2}{7}m\]となるが、nが整数となるためにはmは7の倍数である必要がある。よってm=7とおくと、n=144が自動的に決まる。(m=14とした場合は、k’=2kとくり込むことができる。)まとめると、\[ x=7k+2, \quad y=144k+41\]が 答えである。
(3)は(1)と(2)の結果を応用する問題であり、とても面白い問題だと思う。144の倍数というのは\(144k, \quad x=1,2,3,\cdots \)だから、\(2^4\cdot 3^2 k\)の構造を考えるとよい。(1)の結果として、144の約数の数は15個なので、kの部分をうまく選んで約数が18になるようにすればよい。しかし、問題文で「7で割ったら余りが1」でもある、という制限がつく。これは(2)の\(144x-7y=1\)を書き換えた\(144x = 7y+1\)と同じ意味である。つまり、\(k=1,2,3,\cdots\)と選ぶのではなく、144xに対して、\(x=7k+2, k=0,1,2,\cdots\)という具合に選んでいくのである。ここでも「実験」を行ってみる。k=0のときx=2であり、このとき\(144x = 2^5\cdot 3^2\)という構造を持つ。このときの約数の数は\(6\times 3 = 18\)となって題意に合致する。すなわち、\(144\times 2\)が「約数を18個持つ最小のもの」である。
同じような手順で、次は約数の数が30個のものを探す。k=1,2,3と試していくと、k=3のときその条件が満たされることが簡単に確認できる。このとき\(x=7\cdot 3 + 2 = 23\)であり、\(114\cdot 23 = 2^4\cdot 3^2 \cdot 23\)である。23は素数であるから、約数の数は\(5\times 3\times 2=30\)となるのである。
2018年1月29日月曜日
センター試験の数学2018:幾何の問題(台形の成立条件)
次に第二問[1]の幾何の問題に行ってみよう。四角形の問題であった。AB=5, BC=9, CD=3, AC=6という値が与えられている。この条件で位置が決まるのはA,B,Cの3点であり、点Dは「Cを中心とする半径3の円周上」までは限定できるが、この円周上のどこにあるかは指定できない。それが問題の中心点になっている。
いつものようにpostscriptで作図してみる。まずは座標原点 をAにする。すなわち、A(0,0)とする。次に、Bをx軸に乗せ、B(5,0)とする。ここまでは任意に決めることができる。次に点Cの座標だが、Aを中心とする半径6の円と、Bを中心とする半径9の円の交点として計算できる。すなわち、\[ x^2 + y ^2 = 6^2 \ldots (1), \\ (x-5)^2 + y^2 = 9^2 \ldots (2)\] という連立方程式の解を求めればよい。計算すると、\( C(-2, 4\sqrt{2}) \)を得る。点DはCD=3とだけ指定されているので、Cを中心とする半径3の円周上のどこかにある。すなわち\( D(3\cos\phi-2, 3\sin\phi + 4\sqrt{2})\)となるが、\(\phi\)の値は決められない。
以上の結果をまとめてpostscriptで描いた図が下図である。
この問題の要点は、「四角形ABCDが「台形」となるには、点Dをどこにおけばよいか」という問題である。台形とは、向かい合う辺同士が平行な四角形のことだから、AB//CDの場合と、BC//ADの場合の2つの場合が考えられる。結論を先にいうと、前者の場合は簡単に答えがみつかるが、後者の場合は不可能である。
まずはAB//CDの場合から考えよう。Dを\(\phi=180^\circ\)の場所に置いたときに相当する。この場合を図に表すと、次のようになる。
このときDの座標は\( D(3\cos180^\circ-2, 3\sin180^\circ + 4\sqrt{2})=(-5, 4\sqrt{2})\)となる。対角線BDの長さはピタゴラスの定理を使って\[BD=\sqrt{(-5-5)^2+(4\sqrt{2}-0)^2} = \sqrt{132} = 2\sqrt{33}\]となる。
次にBC//ADの場合を考えてみる。直線CBの傾きは\[\frac{0-4\sqrt{2}}{5-(-5)}=\frac{-2\sqrt{2}}{5}\]であるが、AD//BCとなるためには直線ADの傾きがこの値に等しくなる必要がある。すなわち、\[ \frac{0-(3\sin\phi + 4\sqrt{2})}{0-(3\cos\phi-2)} = \frac{3\sin\phi + 4\sqrt{2}}{3\cos\phi-2} = \frac{-2\sqrt{2}}{5}\]を満たす\(\phi\)を求めることになる。この条件を整理すると、\[15\sin\phi + 6\sqrt{2}\cos\phi = -16\sqrt{2}\]となる。\(\sin^2\phi + \cos^2\phi = 1\)と組み合わせることで\(\phi\)を求めることができるが、これは連立方程式\[ y^2 + x^2 = 1 \\ 15y + 6\sqrt{2}x = -16\sqrt{2}\]の解の条件を調べることに相当する。ただし、\(x=\cos\phi, y=\sin\phi\)とおいた。
xを消去し、yについてまとめると2次式を得る(yを消去し、xについての2次式にしてもよい)。\[\frac{33}{8}y^2 + \frac{20\sqrt{2}}{3}y+\frac{55}{9}=0\] この判別式が負にになれば、実数解が存在しないということになるので、BCに平行な直線ADは円Cと交点を持たないことが証明できる。判別式を計算してみると\[D'=(\frac{10\sqrt{2}}{3})^2-\frac{33}{8}\frac{55}{9}=\frac{1}{8\cdot 9}\left(2^4\cdot 10^2 - 3\cdot 5 \cdot 11^2\right)\] ここで\(11^2 = (10+1)^2 = 10^2 + 20 + 1\)であることを利用すると
\[2^4\cdot 10^2 - 15(10^2 + 20 + 1) = (16-15)10^2 - 3\cdot 5\cdot 20 - 15 = -2\cdot 10^2 - 15 < 0\]となって判別式が負値をとることがわかる。
試験問題では、角度\(\angle ABC \equiv \theta\)についての\(\sin\theta, \cos\theta\)を計算させ、直線BCとADの距離が、円Cの半径(CD=3)よりも大きいことを調べさせている。余弦定理を使えば、簡単に\(\cos\theta = \frac{7}{9}, \sin\theta = \frac{4\sqrt{2}}{9}\)であることがわかる。点Aから直線BCに下ろした垂線の長さが、ADとBCが平行線となる場合の距離に相当するが、これは\(AB\sin\theta=\frac{20\sqrt{2}}{9} > 3=CD\)である。
ちなみに、直線ADがもっとも直線BCから「離れる」のは(つまり、直線ADが直線BCの平行線にもっとも近づくのは)、直線ADが円Cの接線となる場合である。AC=6, CD=3,\(\angle ADC = 90^\circ\)なので、この時三角形ACDは正三角形を半分に切った三角形となる。つまり、\(\angle DCA = 60^\circ, \angle CAD = 30^\circ\)である。これらの性質を用いて、点Dの座標を計算したり、平行条件を調べたりするのも興味深い問題であるが、それは後日の楽しみにとっておくことにしよう。
いつものようにpostscriptで作図してみる。まずは座標原点 をAにする。すなわち、A(0,0)とする。次に、Bをx軸に乗せ、B(5,0)とする。ここまでは任意に決めることができる。次に点Cの座標だが、Aを中心とする半径6の円と、Bを中心とする半径9の円の交点として計算できる。すなわち、\[ x^2 + y ^2 = 6^2 \ldots (1), \\ (x-5)^2 + y^2 = 9^2 \ldots (2)\] という連立方程式の解を求めればよい。計算すると、\( C(-2, 4\sqrt{2}) \)を得る。点DはCD=3とだけ指定されているので、Cを中心とする半径3の円周上のどこかにある。すなわち\( D(3\cos\phi-2, 3\sin\phi + 4\sqrt{2})\)となるが、\(\phi\)の値は決められない。
以上の結果をまとめてpostscriptで描いた図が下図である。
 |
| \(\phi=240^\circ\)とした場合 |
まずはAB//CDの場合から考えよう。Dを\(\phi=180^\circ\)の場所に置いたときに相当する。この場合を図に表すと、次のようになる。
 |
| \(\phi=180^\circ\)とした場合 |
このときDの座標は\( D(3\cos180^\circ-2, 3\sin180^\circ + 4\sqrt{2})=(-5, 4\sqrt{2})\)となる。対角線BDの長さはピタゴラスの定理を使って\[BD=\sqrt{(-5-5)^2+(4\sqrt{2}-0)^2} = \sqrt{132} = 2\sqrt{33}\]となる。
次にBC//ADの場合を考えてみる。直線CBの傾きは\[\frac{0-4\sqrt{2}}{5-(-5)}=\frac{-2\sqrt{2}}{5}\]であるが、AD//BCとなるためには直線ADの傾きがこの値に等しくなる必要がある。すなわち、\[ \frac{0-(3\sin\phi + 4\sqrt{2})}{0-(3\cos\phi-2)} = \frac{3\sin\phi + 4\sqrt{2}}{3\cos\phi-2} = \frac{-2\sqrt{2}}{5}\]を満たす\(\phi\)を求めることになる。この条件を整理すると、\[15\sin\phi + 6\sqrt{2}\cos\phi = -16\sqrt{2}\]となる。\(\sin^2\phi + \cos^2\phi = 1\)と組み合わせることで\(\phi\)を求めることができるが、これは連立方程式\[ y^2 + x^2 = 1 \\ 15y + 6\sqrt{2}x = -16\sqrt{2}\]の解の条件を調べることに相当する。ただし、\(x=\cos\phi, y=\sin\phi\)とおいた。
xを消去し、yについてまとめると2次式を得る(yを消去し、xについての2次式にしてもよい)。\[\frac{33}{8}y^2 + \frac{20\sqrt{2}}{3}y+\frac{55}{9}=0\] この判別式が負にになれば、実数解が存在しないということになるので、BCに平行な直線ADは円Cと交点を持たないことが証明できる。判別式を計算してみると\[D'=(\frac{10\sqrt{2}}{3})^2-\frac{33}{8}\frac{55}{9}=\frac{1}{8\cdot 9}\left(2^4\cdot 10^2 - 3\cdot 5 \cdot 11^2\right)\] ここで\(11^2 = (10+1)^2 = 10^2 + 20 + 1\)であることを利用すると
\[2^4\cdot 10^2 - 15(10^2 + 20 + 1) = (16-15)10^2 - 3\cdot 5\cdot 20 - 15 = -2\cdot 10^2 - 15 < 0\]となって判別式が負値をとることがわかる。
試験問題では、角度\(\angle ABC \equiv \theta\)についての\(\sin\theta, \cos\theta\)を計算させ、直線BCとADの距離が、円Cの半径(CD=3)よりも大きいことを調べさせている。余弦定理を使えば、簡単に\(\cos\theta = \frac{7}{9}, \sin\theta = \frac{4\sqrt{2}}{9}\)であることがわかる。点Aから直線BCに下ろした垂線の長さが、ADとBCが平行線となる場合の距離に相当するが、これは\(AB\sin\theta=\frac{20\sqrt{2}}{9} > 3=CD\)である。
ちなみに、直線ADがもっとも直線BCから「離れる」のは(つまり、直線ADが直線BCの平行線にもっとも近づくのは)、直線ADが円Cの接線となる場合である。AC=6, CD=3,\(\angle ADC = 90^\circ\)なので、この時三角形ACDは正三角形を半分に切った三角形となる。つまり、\(\angle DCA = 60^\circ, \angle CAD = 30^\circ\)である。これらの性質を用いて、点Dの座標を計算したり、平行条件を調べたりするのも興味深い問題であるが、それは後日の楽しみにとっておくことにしよう。
2018年1月28日日曜日
センター試験の数学2018: 集合の包含関係の問題(2)
次は(2)を解いて見よう。ちなみに、MathJaXはなかなか使い勝手がよかったので、これからも使っていこうと思う。
(2)は必要条件とか、十分条件とかを判定する問題である。どちらがどちらか混乱し、間違えやすいので、ここでケリをつけておきたい。
与えられた条件は4つあるが、これらの条件に合致する「集合」の包含関係を考えることで、間違えることはなくなる。まずは、それぞれの条件を見てみよう。今年は、次の条件を満たす実数xの集合である。
\[ p: |x-2| > 2, \ q: x < 0, \ r: x > 4, \ s: \sqrt{x^2} > 4\]
条件qとrが指定する集合QとRは文字どおりの集合であり、特に分析する必要はない。条件pを満たす集合Pは、不等式を解くことにより、4より大きいか、あるいは0より小さい実数の集合となる。すなわち\[ p: x < 0, x > 4\]である。これはP=Q+R、あるいは\(P=Q\cup R, Q \cap R = \emptyset\)と表せる。
一方、条件sは\( x < -4, 4 < x \)と書き直すことができるので、\( S \supset R \)であることは明らかである。
さて最初の問題は、「qまたはr」という条件が、条件pに対するどんな条件になっているか判定する問題である。これは\( Q \cup R \)という集合と、集合Pの包含関係を見極めることから始まる。上ですでに考察したように、\( Q \cup R = P \)という関係が成り立っているので、これらの集合は等価な集合である。このような場合は、「必要十分条件」に相当する。英語でいうところの"if and only if"というやつである。つまり、"p holds if and only if q or r holds"と書き直せる。
次の問題は、条件sと条件rの包含関係である。これも上で考察したように\( S \supset R \)である。大きな集合に対応する命題は、より小さな集合に対応する命題が成立するための「必要条件」であり、その逆が「十分条件」である。この場合はSの方が大きな集合になっているので、s→rにおけるsはrの「必要条件」である。つまり "r holds if s holds"である。
したがって、ケ:(2), コ:(0)が正解となる。
(2)は必要条件とか、十分条件とかを判定する問題である。どちらがどちらか混乱し、間違えやすいので、ここでケリをつけておきたい。
与えられた条件は4つあるが、これらの条件に合致する「集合」の包含関係を考えることで、間違えることはなくなる。まずは、それぞれの条件を見てみよう。今年は、次の条件を満たす実数xの集合である。
\[ p: |x-2| > 2, \ q: x < 0, \ r: x > 4, \ s: \sqrt{x^2} > 4\]
条件qとrが指定する集合QとRは文字どおりの集合であり、特に分析する必要はない。条件pを満たす集合Pは、不等式を解くことにより、4より大きいか、あるいは0より小さい実数の集合となる。すなわち\[ p: x < 0, x > 4\]である。これはP=Q+R、あるいは\(P=Q\cup R, Q \cap R = \emptyset\)と表せる。
一方、条件sは\( x < -4, 4 < x \)と書き直すことができるので、\( S \supset R \)であることは明らかである。
さて最初の問題は、「qまたはr」という条件が、条件pに対するどんな条件になっているか判定する問題である。これは\( Q \cup R \)という集合と、集合Pの包含関係を見極めることから始まる。上ですでに考察したように、\( Q \cup R = P \)という関係が成り立っているので、これらの集合は等価な集合である。このような場合は、「必要十分条件」に相当する。英語でいうところの"if and only if"というやつである。つまり、"p holds if and only if q or r holds"と書き直せる。
次の問題は、条件sと条件rの包含関係である。これも上で考察したように\( S \supset R \)である。大きな集合に対応する命題は、より小さな集合に対応する命題が成立するための「必要条件」であり、その逆が「十分条件」である。この場合はSの方が大きな集合になっているので、s→rにおけるsはrの「必要条件」である。つまり "r holds if s holds"である。
したがって、ケ:(2), コ:(0)が正解となる。
センター試験の数学2018: 集合の包含関係の問題(1)
今年も試験の季節がやってきた。
センター試験の問題が公表されたので、小手調べに幾つか解いてみよう。毎年、最後まで解ききらないうちに、二次試験が始まってしまって、いつも中途半端となり反省している。今年はそうならないように頑張ってみようと思う。中途半端となる最大の原因は数式の入力だ。今まではLaTeXiTを使ってpngファイルを作成し、それを画像ファイルとして貼り付けていた。今回からは、MathJaXというJavaScriptの拡張機能を使って、直接LaTeXコマンドをhtmlで使う方法を導入してみようと思う。果たして、これでどのくらい時間の節約になるか、興味津々である。
まずは、毎年出題される論理問題から始めて見たい(第1問の[2])。なかなか良い問題が出るので、注目しているセクションでもある。
まず考える全体集合(英語ではUniversal setというらしいが、数学者によっては"Universe"、つまり「宇宙」という用語を用いることもある。しかし、これを真似して物理の論文でuniverseを使ったら、「なんで、量子力学の論文の中に「宇宙」が出てくるんだ?!」とひどく怒られたことがある)の定義として、\[ U=\{x|x \le 20, x \in N\}\] が与えられる。Nは自然数全体を表す。Uに含まれる3つの部分集合A,B,Cの包含関係(inclusion, containment)を議論しようという問題である。
Aは20の約数である。素因数分解すると\( 20 = 2^2 \cdot 5\)であるが、因数としては1が含まれることも注意しておこう(1は素数ではないので、「素因数」分解には含まれないが、「因数」分解には含まれる)。したがって、上の素因数分解を利用し、可能な因数を数え上げると、\[A=\{ 1, 2, 2^2, 5, 2\cdot 5, 2^2\cdot 5\}=\{1,2,4,5,10,20\} \]となり、Aに含まれる元(element、集合に含まれる「要素」のこと)の数(群論では位数=orderというが、集合論では基数あるいは濃度、cardinalityというらしい)は6となる。
Bは20より小さい、3の倍数である。すなわち\[B=\{3,6,9,12,15,18\}\]となり、元の数(基数)は6である。
Cは20以下の偶数だから \[C=\{2,4,6,8,10,12,14,16,18,20\}\]となり、基数=10である。CはUの半分を占める。Cの補集合\( U-C\)を\( C^c\)と表すと、\(U=C+C^c\)と分解できる。当然、\(C^c\)は20以下の奇数の集合となる。また、\(C\cap C^c=\emptyset\)であり、\(C\cup C^c = U\)である。(ちなみに、日本の高校数学では補集合は\(\bar{C}\)と表すが、世界に出るとこの記号の意味はわかってもらえないことが多いので注意が必要だ。cという記号はcomplementary set、つまり補集合の「補」を表す英語の頭文字である。)
Aには奇数が含まれているので、\(A\subset C\)というのは当然ながら「偽」である。 また、Aの中には3の倍数は一つも含まれていないので、AとCの共通元の集合は空集合であることも明らかである。したがって、\(A\cap C=\emptyset\)というのは「真」である。
A,B,CおよびUの包含関係を図にすることは簡単にできる。
この集合の包含関係で重要なのは、すべての集合が奇数/偶数によって直和分解できることだ。例えば、\(A\cap C = \{2,4,10,20\}, A\cap C^c =\{1,5\}\)だから、\(A=(A\cap C) + (A\cap C^c) = A\cap(C+C^c) = A\cap U = A(∴ A\subset U)\)である。全体集合Uが、偶数の部分集合Cと奇数の部分集合\(C^c\)に直和分解できることを認識するのが重要である。
さて\((A\cup C)\cap B\)である。直接やっても解けるのだが、\(A\cup C\)が面倒臭い。これは偶数全体に、Aの奇数部分\(A\cap C^c\)を「足した」ものであるから、{1,5}+{2,4,6,....,20}である。これとBの共通部分というのが最終的な答えであるが、Bは3の倍数である。{1,5}に3の倍数は存在しないので、\( C\cap B\)が答えであり、それは偶数の3の倍数であるから{6,12,18}の3つである。したがって、命題(c)は「真」である。
実は、以上の考え方は、論理式の展開の流れをなぞったものになっている。展開すると、
\[ (A\cup C)\cap B = (A\cap B)\cup (C\cap B) = \emptyset \cup (C\cap B) = C\cap B\]となる。
最後の問題は、2つの包含関係式の比較である。左辺は\( (A^c\cap C) \cup B\)、右辺は\( A^c\cap (B \cup C)\)であり、これらが等価かどうか判断せよ、という問題である。論理式を展開してもあまり見通しは良くない感じである。Cと\(C^c\)が任意の集合を2分割するという性質を使えば、\( ... \cap C\)という関係式がある部分をできるだけ生かしたい。
左辺にはこの関係があるので、さっそく適用して見る。\( (A^c \cap C)\)だから、Aに含まれていない偶数の集合であり、それは{6,12,18}+{8,14,16}である。最初の集合はBに含まれている偶数、後者はBに含まれていない偶数である。Bとのunionを最後に考えれば、Bの奇数部分{3,9,15}を足した{6,12,18}+{8,14,16}+{3,9,5}=B+{8,14,16}、つまり3の倍数(20以下)と{8,14,16}が該当する集合となる。
右辺を次に考えてみる。こちらは展開してみると\( A^c \cap (B \cup C) = (A^c \cap B) \cup (A^c \cap C)\)である。AとBは重なりを持たないので、\(A^c \cap B = B\)である。したがって、Bと{6,12,18}+{8,14,16}のunionはB+{8,14,16}となって、左辺と同じ集合になる。
つまり[ク]の答えは(0)正、正である。 この問題を正しく解く秘訣は、やはり包含関係の図を描くということに尽きると思う。加えて,\(U=C+C^c\)という関係にも注意がいけば、早く解くことができる。
センター試験の問題が公表されたので、小手調べに幾つか解いてみよう。毎年、最後まで解ききらないうちに、二次試験が始まってしまって、いつも中途半端となり反省している。今年はそうならないように頑張ってみようと思う。中途半端となる最大の原因は数式の入力だ。今まではLaTeXiTを使ってpngファイルを作成し、それを画像ファイルとして貼り付けていた。今回からは、MathJaXというJavaScriptの拡張機能を使って、直接LaTeXコマンドをhtmlで使う方法を導入してみようと思う。果たして、これでどのくらい時間の節約になるか、興味津々である。
まずは、毎年出題される論理問題から始めて見たい(第1問の[2])。なかなか良い問題が出るので、注目しているセクションでもある。
まず考える全体集合(英語ではUniversal setというらしいが、数学者によっては"Universe"、つまり「宇宙」という用語を用いることもある。しかし、これを真似して物理の論文でuniverseを使ったら、「なんで、量子力学の論文の中に「宇宙」が出てくるんだ?!」とひどく怒られたことがある)の定義として、\[ U=\{x|x \le 20, x \in N\}\] が与えられる。Nは自然数全体を表す。Uに含まれる3つの部分集合A,B,Cの包含関係(inclusion, containment)を議論しようという問題である。
Aは20の約数である。素因数分解すると\( 20 = 2^2 \cdot 5\)であるが、因数としては1が含まれることも注意しておこう(1は素数ではないので、「素因数」分解には含まれないが、「因数」分解には含まれる)。したがって、上の素因数分解を利用し、可能な因数を数え上げると、\[A=\{ 1, 2, 2^2, 5, 2\cdot 5, 2^2\cdot 5\}=\{1,2,4,5,10,20\} \]となり、Aに含まれる元(element、集合に含まれる「要素」のこと)の数(群論では位数=orderというが、集合論では基数あるいは濃度、cardinalityというらしい)は6となる。
Bは20より小さい、3の倍数である。すなわち\[B=\{3,6,9,12,15,18\}\]となり、元の数(基数)は6である。
Cは20以下の偶数だから \[C=\{2,4,6,8,10,12,14,16,18,20\}\]となり、基数=10である。CはUの半分を占める。Cの補集合\( U-C\)を\( C^c\)と表すと、\(U=C+C^c\)と分解できる。当然、\(C^c\)は20以下の奇数の集合となる。また、\(C\cap C^c=\emptyset\)であり、\(C\cup C^c = U\)である。(ちなみに、日本の高校数学では補集合は\(\bar{C}\)と表すが、世界に出るとこの記号の意味はわかってもらえないことが多いので注意が必要だ。cという記号はcomplementary set、つまり補集合の「補」を表す英語の頭文字である。)
Aには奇数が含まれているので、\(A\subset C\)というのは当然ながら「偽」である。 また、Aの中には3の倍数は一つも含まれていないので、AとCの共通元の集合は空集合であることも明らかである。したがって、\(A\cap C=\emptyset\)というのは「真」である。
A,B,CおよびUの包含関係を図にすることは簡単にできる。
この集合の包含関係で重要なのは、すべての集合が奇数/偶数によって直和分解できることだ。例えば、\(A\cap C = \{2,4,10,20\}, A\cap C^c =\{1,5\}\)だから、\(A=(A\cap C) + (A\cap C^c) = A\cap(C+C^c) = A\cap U = A(∴ A\subset U)\)である。全体集合Uが、偶数の部分集合Cと奇数の部分集合\(C^c\)に直和分解できることを認識するのが重要である。
さて\((A\cup C)\cap B\)である。直接やっても解けるのだが、\(A\cup C\)が面倒臭い。これは偶数全体に、Aの奇数部分\(A\cap C^c\)を「足した」ものであるから、{1,5}+{2,4,6,....,20}である。これとBの共通部分というのが最終的な答えであるが、Bは3の倍数である。{1,5}に3の倍数は存在しないので、\( C\cap B\)が答えであり、それは偶数の3の倍数であるから{6,12,18}の3つである。したがって、命題(c)は「真」である。
実は、以上の考え方は、論理式の展開の流れをなぞったものになっている。展開すると、
\[ (A\cup C)\cap B = (A\cap B)\cup (C\cap B) = \emptyset \cup (C\cap B) = C\cap B\]となる。
最後の問題は、2つの包含関係式の比較である。左辺は\( (A^c\cap C) \cup B\)、右辺は\( A^c\cap (B \cup C)\)であり、これらが等価かどうか判断せよ、という問題である。論理式を展開してもあまり見通しは良くない感じである。Cと\(C^c\)が任意の集合を2分割するという性質を使えば、\( ... \cap C\)という関係式がある部分をできるだけ生かしたい。
左辺にはこの関係があるので、さっそく適用して見る。\( (A^c \cap C)\)だから、Aに含まれていない偶数の集合であり、それは{6,12,18}+{8,14,16}である。最初の集合はBに含まれている偶数、後者はBに含まれていない偶数である。Bとのunionを最後に考えれば、Bの奇数部分{3,9,15}を足した{6,12,18}+{8,14,16}+{3,9,5}=B+{8,14,16}、つまり3の倍数(20以下)と{8,14,16}が該当する集合となる。
右辺を次に考えてみる。こちらは展開してみると\( A^c \cap (B \cup C) = (A^c \cap B) \cup (A^c \cap C)\)である。AとBは重なりを持たないので、\(A^c \cap B = B\)である。したがって、Bと{6,12,18}+{8,14,16}のunionはB+{8,14,16}となって、左辺と同じ集合になる。
つまり[ク]の答えは(0)正、正である。 この問題を正しく解く秘訣は、やはり包含関係の図を描くということに尽きると思う。加えて,\(U=C+C^c\)という関係にも注意がいけば、早く解くことができる。
登録:
投稿 (Atom)