センター試験の数学2018:第5問（幾何はすべて代数幾何で解く）

公式や定理をたくさん覚え、それをどう使いこなすかというのが幾何の解き方だとすると、定理を忘れてしまうとどうにも手が出せない。余弦定理、正弦定理、メネラウスの定理、チェバの定理、いろいろある。今回のセンター試験の問題５では「角の二等分線の定理」とやらを使う問題が出た。しかし、そんな「マイナーな定理」を忘れてしまった人はどうすればよいのだろうか？

私の方針は以前より首尾一貫している。デカルトの編み出した代数幾何である。 幾何の問題を代数の問題に書き直すのである。こうすれば、定理を忘れた時には、連立方程式や判別式の計算をするだけで答えが手にはいる。

代数幾何学でもっとも重要なのは、どのような座標系を選ぶかである。うまい座標系を選べばあっという間に解にたどり着ける問題でも、まずい座標系で解き始めると本当に苦労することがある。これは物理学でも同じことで、最初に選んだ座標系では手も出せないような多体問題が、カノニカル変換によって座標変換するとあっという間に解けてしまったりする。超電導のBCS理論で出てくるボゴリウボフ変換がそのよい例だ。「実粒子」ではなく、見方を変えて「準粒子」を用いて問題を解いた方が見通しがよくなるのである。

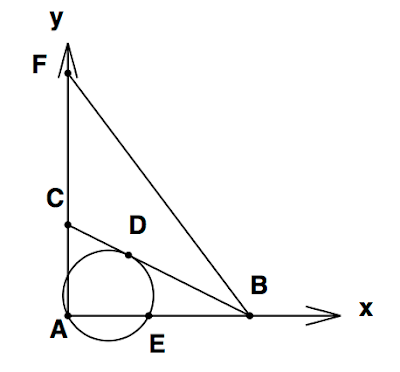
さて、センター試験の第５問では直角三角形が出てくる。２次元のデカルト座標系 は直交座標だから、原点に点Aを合わせ、線分ABがx軸に、線分ACがy軸になるように選ぶと自然な座標系の選び方となる。

次に、点A（原点）を通り、直線BCに接するような円を考え、この円とABの交点のうち、Aでない点をEとする。したがって、O=A(0,0), B=(2,0), C=(0,1)となる。問題ではいきなりBDの長さを計算させているが、ここではあえて、円の方程式を求めた後、連立方程式を用いてDとEの座標を計算してみよう。まず円の方程式を\[ (x-p)^2 + (y-q)^2 = r^2\]とおく。この円は原点を通るので\[p^2 + q^2 = r^2\]であることがまず示せる。したがって、円の方程式は\[x^2 -2px + y^2 - 2qy = 0\]となる。次に、直線BCの方程式は\[y= -\frac{1}{2}x + 1\]であることはすぐにわかる。この直線と円は接するというので、連立方程式から得られる二次方程式の判別式が０とならねばならない。yを消去して、xについての２次式を計算すると、\[5x^2 - 4(2p-q+1)x+4(1-2q)=0\]を得る。判別式が０となるので\[ \{2(2p-q+1)\}^2 - 5\cdot 4(1-2q) = 0\]である。最後に、この接点は点Dに他ならず、それは直線BCと直線ADの交点である。直線ADの方程式は\[y=x\]に他ならない（直角の２等分線だから）。したがって、連立方程式を解くことで、ADとBCの交点の座標Dが求まり、それはD(2/3,2/3)となる。円の方程式にこの値を代入すると、\[p+q = \frac{2}{3}\]を得る。これを判別式=0の条件に代入してqを消去すると、pに関する二次式\[\left(3p-\frac{4}{3}\right)^2=0\]を得るが、この方程式の解は簡単に求まって\(p=\frac{4}{9}\)の重解である。また\(q=\frac{2}{9}\)であることも容易に計算できる。同様に、円の半径の自乗は\(r^2 = p^2  + q^2 =\frac{20}{81}\)と計算される。以上より、円の方程式は\[\left(x-\frac{4}{9}\right)^2 + \left(y-\frac{2}{9}\right)^2 = \frac{20}{81}\]である。

点Eの座標は円がx軸と交わる場所であるから、上の方程式にy=0を代入し、xについての方程式\[\left(x-\frac{4}{9}\right)^2 + \frac{4}{81} = \frac{20}{81}\]を解けばよい。この方程式の解は\(x=0, \frac{8}{9}\)となるが、最初の解は点Aに相当するので、２つ目の解を選ぶ。つまり\(E(\frac{8}{9},0)\)である。

点A,B,C,D,Eのすべての座標がわかってしまったので、あとはピタゴラスの定理を駆使して２点間の距離を計算するだけで、線分の長さはすべて手にはいる！これが「代数」幾何の強みに他ならない。（もちろん、幾何の定理を知っていれば試験中にもっと早く計算できるかもしれない。しかし、その定理を覚えるためには勉強時間を長くしなくてはならないし、万が一忘れてしまったらその勉強時間は無駄になってしまう。）

ではいつものように、以上で得た情報を元にpostscriptで作図してみよう。

つづく問題では、直線EDの表す方程式のy切片（点F)に相当する値が必要となる。点Fの座標を求めておこう。点EとDを通る直線の方程式は\[ y = \frac{2/3}{2/3-8/9}(x-8/9)=-3x+\frac{8}{3}\]である。したがって、\(F(0,\frac{8}{3})\)となる。

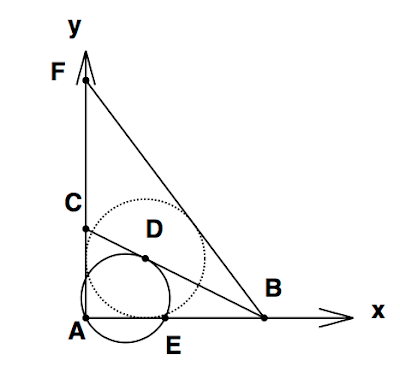
最後の問題は、重心、外心、内心の３種類の点の定義を覚えているかどうか、というある意味「つまらない質問」である。が、これも代数幾何でなんとか突破できると思う。答えは内心であるが、それは\(\angle ABC = \angle FBC\)を示すことで証明できる。

ちなみに、重心や外心ならば、AC=FCとなっているはずだが、明らかにそれは成り立っていない。さらに外心ならばAC=FCであるのみならず、CBはx軸に平行な直線であるべきだが、あきらかに傾きを持っている。重心と外心はしたがって候補から簡単に外れる。消去法で答えは内心となるのだが、これでは「問題が解ける」だけであって、数学の研究とはならない。積極的な方法(active approach)で内心であることを示そう。

方法はいろいろあるが、一つの方法としては\[\tan\angle ABF = \frac{2\tan\angle ABC}{1-\tan^2\angle ABC}\]を確認することである。これは簡単に確認できる。

ちなみに、この内心を中心とする内接円は\[(x-\frac{2}{3})^2+(y-\frac{2}{3})^2 = (\frac{2}{3})^2\]で表される。

センター試験の数学2018:第４問

この整数問題は非常によい問題で、頭を動かして、手を動かして、その場で「考える」必要があるだろう。決まり切ったパターンで乗り切ろうとしてもなかなかうまくいかず、諦めてしまう人は多いと思うが、本来合格させたいと思う学生はこういう問題を解いてくる学生である。チャレンジした学生には「ボーナス点」を与えてもよいのではないだろうか？問題は３つのセクションに分かれていて、それぞれが独立の要素もありつつ、お互いに関連している。最初の部分でこけるとその後は全滅してしまうので、そこがこの問題の「問題点」かもしれない。

(1)素因数分解させた後に、因数分解（約数）の組み合わせの数を調べさせる問題。整数の問題と数え上げの問題が混じった、このタイプの問題を好きな人（出題者=大学の先生）は多いと思う。

今年のセンター試験では114が選ばれた。素因数分解は、\[114 = 2^4\cdot 3^2\]である。114の約数をすべて数え上げると幾つになるか？注意すべきは、1と114も約数に含まれるということ。

約数は\(2^m\cdot 3^n\)と表せる。ただし、\(m=0,1,2,3,4; n=0,1,2\)である。結局、約数の総数は、(m,n)の組み合わせ総数の数と同じである。 したがって、\(5\times 3=15\)が答えである。

(2) さきほど素因数分解した114が再び出てくる。今度は素数7との関わりを考えつつ、144と7が同時に関係する公倍数とか公約数について、一次式と絡めて解く良い問題である。与えられたのは\[144x-7y=1\]である。一見して一次関数のように見えるが、(x,y)は整数の組であることに注意を払う必要がある。つまり、このグラフは原子の一次元結晶のように点と点が離れて並んでいる「物体」であって、連続体としての「棒」が伸びているイメージを持ってはならない。

x,yについては負の整数となる可能性も考慮すべきだが、簡単な分析から不要であることがすぐにわかる。ただ、試験中にこの分析をしていると時間が取られてしまうし、その努力が評価もされないので、解答欄の大きさを見て（負の数なら符号の分の解答欄があるはず）正の整数と決めつけることになろう。ただ、こういう姿勢が染み付くと、大学に入ってから苦しむことになるので、本番以外では丁寧に分析して解く癖を身につけておくべきだ。ただ、問題には「xの絶対値が最小」という具合に、負の数を考えないように釘を刺している点には注意したい。まあ、受験上でこういう微妙な表現に気づくのは至難の技だとは思う。「試験慣れ」というのはこういうところであって、試験の点が高いことが学力の高さを意味するとは限らない、というのがよく出る場所だろう。（ボーアはこういう問題が得意だろうが、アインシュタインは苦手だろう。）

さて、|x|に着目するので |x|=0,1,2あたりを最初に当てはめて「実験的に」考えて見よう。このように「例題」を使って一般化を試みることは、数学者もよく使う方法だ。恥ずかしいことはひとつもない。まずx=0は当てはまらないことがすぐにわかる。つぎにx=1とx=-1を考えてみよう。x=-1の場合、\(7y=-144-1=-145=5\cdot 29\)であるから、整数解yは見つからない。29は素数である。x=1の場合は、\(7y = 144-1 =143 = 11\cdot 13\)となり、やはり7以外の素数同士の積が素数７の倍数となることはないので、これも場外される。x=-2がうまくいかないのは省略するとして、x=2の場合を試してみる。実はこれが正解になっている。\[ 7y = 144\cdot 2 -1 = 287 = 7\cdot 41\]
(x,y)=(2,41)が正解である。

次は、上の線形関係式を満たす一般の(x,y)の形を見つける問題だが、出題者の好意により\[x=mk+2, \quad y = nk + 41\]という形が与えられているから、これを最大限に利用しよう。k=0の場合が、上で求めた場合(x,y)=(2,41)に相当する。問題になっているのは整数m,nの値を決めることである。まずは、上の形は線形関係に代入する。定数部分の差が１となるのは（上の問題で）わかっているので、mとnが満たすべき関係として\(144m-7n=0\)を得る。因数分解の結果を用いると\[ n = \frac{2^4\cdot 3^2}{7}m\]となるが、nが整数となるためにはmは７の倍数である必要がある。よってm=7とおくと、n=144が自動的に決まる。（m=14とした場合は、k’=2kとくり込むことができる。）まとめると、\[ x=7k+2, \quad y=144k+41\]が 答えである。

(3)は(1)と(2)の結果を応用する問題であり、とても面白い問題だと思う。144の倍数というのは\(144k, \quad x=1,2,3,\cdots \)だから、\(2^4\cdot 3^2 k\)の構造を考えるとよい。(1)の結果として、144の約数の数は15個なので、kの部分をうまく選んで約数が18になるようにすればよい。しかし、問題文で「７で割ったら余りが１」でもある、という制限がつく。これは(2)の\(144x-7y=1\)を書き換えた\(144x = 7y+1\)と同じ意味である。つまり、\(k=1,2,3,\cdots\)と選ぶのではなく、144xに対して、\(x=7k+2, k=0,1,2,\cdots\)という具合に選んでいくのである。ここでも「実験」を行ってみる。k=0のときx=2であり、このとき\(144x = 2^5\cdot 3^2\)という構造を持つ。このときの約数の数は\(6\times 3 = 18\)となって題意に合致する。すなわち、\(144\times 2\)が「約数を18個持つ最小のもの」である。

同じような手順で、次は約数の数が30個のものを探す。k=1,2,3と試していくと、k=3のときその条件が満たされることが簡単に確認できる。このとき\(x=7\cdot 3 + 2 = 23\)であり、\(114\cdot 23 = 2^4\cdot 3^2 \cdot 23\)である。23は素数であるから、約数の数は\(5\times 3\times 2=30\)となるのである。

センター試験の数学2018：幾何の問題（台形の成立条件）

次に第二問[1]の幾何の問題に行ってみよう。四角形の問題であった。AB=5, BC=9, CD=3, AC=6という値が与えられている。この条件で位置が決まるのはA,B,Cの３点であり、点Dは「Cを中心とする半径3の円周上」までは限定できるが、この円周上のどこにあるかは指定できない。それが問題の中心点になっている。

いつものようにpostscriptで作図してみる。まずは座標原点 をAにする。すなわち、A(0,0)とする。次に、Bをx軸に乗せ、B(5,0)とする。ここまでは任意に決めることができる。次に点Cの座標だが、Aを中心とする半径6の円と、Bを中心とする半径9の円の交点として計算できる。すなわち、\[ x^2 + y ^2 = 6^2 \ldots (1), \\ (x-5)^2 + y^2 = 9^2 \ldots (2)\] という連立方程式の解を求めればよい。計算すると、\( C(-2, 4\sqrt{2}) \)を得る。点DはCD=3とだけ指定されているので、Cを中心とする半径3の円周上のどこかにある。すなわち\( D(3\cos\phi-2, 3\sin\phi + 4\sqrt{2})\)となるが、\(\phi\)の値は決められない。

以上の結果をまとめてpostscriptで描いた図が下図である。

\(\phi=240^\circ\)とした場合

この問題の要点は、「四角形ABCDが「台形」となるには、点Dをどこにおけばよいか」という問題である。台形とは、向かい合う辺同士が平行な四角形のことだから、AB//CDの場合と、BC//ADの場合の２つの場合が考えられる。結論を先にいうと、前者の場合は簡単に答えがみつかるが、後者の場合は不可能である。

まずはAB//CDの場合から考えよう。Dを\(\phi=180^\circ\)の場所に置いたときに相当する。この場合を図に表すと、次のようになる。

\(\phi=180^\circ\)とした場合

このときDの座標は\( D(3\cos180^\circ-2, 3\sin180^\circ + 4\sqrt{2})=(-5, 4\sqrt{2})\)となる。対角線BDの長さはピタゴラスの定理を使って\[BD=\sqrt{(-5-5)^2+(4\sqrt{2}-0)^2} = \sqrt{132} = 2\sqrt{33}\]となる。

次にBC//ADの場合を考えてみる。直線CBの傾きは\[\frac{0-4\sqrt{2}}{5-(-5)}=\frac{-2\sqrt{2}}{5}\]であるが、AD//BCとなるためには直線ADの傾きがこの値に等しくなる必要がある。すなわち、\[ \frac{0-(3\sin\phi + 4\sqrt{2})}{0-(3\cos\phi-2)} = \frac{3\sin\phi + 4\sqrt{2}}{3\cos\phi-2} = \frac{-2\sqrt{2}}{5}\]を満たす\(\phi\)を求めることになる。この条件を整理すると、\[15\sin\phi + 6\sqrt{2}\cos\phi = -16\sqrt{2}\]となる。\(\sin^2\phi + \cos^2\phi = 1\)と組み合わせることで\(\phi\)を求めることができるが、これは連立方程式\[ y^2 + x^2 = 1 \\ 15y + 6\sqrt{2}x = -16\sqrt{2}\]の解の条件を調べることに相当する。ただし、\(x=\cos\phi, y=\sin\phi\)とおいた。

xを消去し、yについてまとめると２次式を得る(yを消去し、xについての２次式にしてもよい）。\[\frac{33}{8}y^2 + \frac{20\sqrt{2}}{3}y+\frac{55}{9}=0\]　この判別式が負にになれば、実数解が存在しないということになるので、BCに平行な直線ADは円Cと交点を持たないことが証明できる。判別式を計算してみると\[D'=(\frac{10\sqrt{2}}{3})^2-\frac{33}{8}\frac{55}{9}=\frac{1}{8\cdot 9}\left(2^4\cdot 10^2 - 3\cdot 5 \cdot 11^2\right)\]　ここで\(11^2 = (10+1)^2 = 10^2 + 20 + 1\)であることを利用すると
\[2^4\cdot 10^2 - 15(10^2 + 20 + 1) = (16-15)10^2 - 3\cdot 5\cdot 20 - 15 = -2\cdot 10^2 - 15 < 0\]となって判別式が負値をとることがわかる。

試験問題では、角度\(\angle ABC \equiv \theta\)についての\(\sin\theta, \cos\theta\)を計算させ、直線BCとADの距離が、円Cの半径(CD=３)よりも大きいことを調べさせている。余弦定理を使えば、簡単に\(\cos\theta = \frac{7}{9}, \sin\theta = \frac{4\sqrt{2}}{9}\)であることがわかる。点Aから直線BCに下ろした垂線の長さが、ADとBCが平行線となる場合の距離に相当するが、これは\(AB\sin\theta=\frac{20\sqrt{2}}{9} > 3=CD\)である。

ちなみに、直線ADがもっとも直線BCから「離れる」のは（つまり、直線ADが直線BCの平行線にもっとも近づくのは）、直線ADが円Cの接線となる場合である。AC=6, CD=3,\(\angle ADC = 90^\circ\)なので、この時三角形ACDは正三角形を半分に切った三角形となる。つまり、\(\angle DCA = 60^\circ, \angle CAD = 30^\circ\)である。これらの性質を用いて、点Dの座標を計算したり、平行条件を調べたりするのも興味深い問題であるが、それは後日の楽しみにとっておくことにしよう。

センター試験の数学2018: 集合の包含関係の問題(2)

次は(2)を解いて見よう。ちなみに、MathJaXはなかなか使い勝手がよかったので、これからも使っていこうと思う。

(2)は必要条件とか、十分条件とかを判定する問題である。どちらがどちらか混乱し、間違えやすいので、ここでケリをつけておきたい。

与えられた条件は４つあるが、これらの条件に合致する「集合」の包含関係を考えることで、間違えることはなくなる。まずは、それぞれの条件を見てみよう。今年は、次の条件を満たす実数xの集合である。

\[ p: |x-2| > 2, \ q: x < 0, \ r: x > 4, \ s: \sqrt{x^2} > 4\]

条件qとrが指定する集合QとRは文字どおりの集合であり、特に分析する必要はない。条件pを満たす集合Pは、不等式を解くことにより、4より大きいか、あるいは０より小さい実数の集合となる。すなわち\[ p: x < 0, x > 4\]である。これはP=Q+R、あるいは\(P=Q\cup R, Q \cap R = \emptyset\)と表せる。

一方、条件sは\( x < -4, 4 < x \)と書き直すことができるので、\( S \supset R \)であることは明らかである。

さて最初の問題は、「qまたはr」という条件が、条件pに対するどんな条件になっているか判定する問題である。これは\( Q \cup R \)という集合と、集合Pの包含関係を見極めることから始まる。上ですでに考察したように、\( Q \cup R = P \)という関係が成り立っているので、これらの集合は等価な集合である。このような場合は、「必要十分条件」に相当する。英語でいうところの"if and only if"というやつである。つまり、"p holds if and only if q or r holds"と書き直せる。

次の問題は、条件sと条件rの包含関係である。これも上で考察したように\( S \supset R \)である。大きな集合に対応する命題は、より小さな集合に対応する命題が成立するための「必要条件」であり、その逆が「十分条件」である。この場合はSの方が大きな集合になっているので、s→rにおけるsはrの「必要条件」である。つまり "r holds if s holds"である。

したがって、ケ：(2),　コ：(0)が正解となる。

センター試験の数学2018: 集合の包含関係の問題(1)

今年も試験の季節がやってきた。

センター試験の問題が公表されたので、小手調べに幾つか解いてみよう。毎年、最後まで解ききらないうちに、二次試験が始まってしまって、いつも中途半端となり反省している。今年はそうならないように頑張ってみようと思う。中途半端となる最大の原因は数式の入力だ。今まではLaTeXiTを使ってpngファイルを作成し、それを画像ファイルとして貼り付けていた。今回からは、MathJaXというJavaScriptの拡張機能を使って、直接LaTeXコマンドをhtmlで使う方法を導入してみようと思う。果たして、これでどのくらい時間の節約になるか、興味津々である。

まずは、毎年出題される論理問題から始めて見たい（第１問の[2])。なかなか良い問題が出るので、注目しているセクションでもある。

まず考える全体集合（英語ではUniversal setというらしいが、数学者によっては"Universe"、つまり「宇宙」という用語を用いることもある。しかし、これを真似して物理の論文でuniverseを使ったら、「なんで、量子力学の論文の中に「宇宙」が出てくるんだ？！」とひどく怒られたことがある）の定義として、\[ U=\{x|x \le 20, x \in N\}\]　が与えられる。Nは自然数全体を表す。Uに含まれる３つの部分集合A,B,Cの包含関係(inclusion, containment)を議論しようという問題である。

Aは20の約数である。素因数分解すると\( 20 = 2^2 \cdot 5\)であるが、因数としては1が含まれることも注意しておこう（1は素数ではないので、「素因数」分解には含まれないが、「因数」分解には含まれる）。したがって、上の素因数分解を利用し、可能な因数を数え上げると、\[A=\{ 1, 2, 2^2, 5, 2\cdot 5, 2^2\cdot 5\}=\{1,2,4,5,10,20\} \]となり、Aに含まれる元(element、集合に含まれる「要素」のこと）の数（群論では位数=orderというが、集合論では基数あるいは濃度、cardinalityというらしい）は6となる。

Bは20より小さい、３の倍数である。すなわち\[B=\{3,6,9,12,15,18\}\]となり、元の数（基数）は６である。

Cは20以下の偶数だから \[C=\{2,4,6,8,10,12,14,16,18,20\}\]となり、基数=10である。CはUの半分を占める。Cの補集合\( U-C\)を\( C^c\)と表すと、\(U=C+C^c\)と分解できる。当然、\(C^c\)は20以下の奇数の集合となる。また、\(C\cap C^c=\emptyset\)であり、\(C\cup C^c = U\)である。（ちなみに、日本の高校数学では補集合は\(\bar{C}\)と表すが、世界に出るとこの記号の意味はわかってもらえないことが多いので注意が必要だ。cという記号はcomplementary set、つまり補集合の「補」を表す英語の頭文字である。）

Aには奇数が含まれているので、\(A\subset C\)というのは当然ながら「偽」である。 また、Aの中には３の倍数は一つも含まれていないので、AとCの共通元の集合は空集合であることも明らかである。したがって、\(A\cap C=\emptyset\)というのは「真」である。

 A,B,CおよびUの包含関係を図にすることは簡単にできる。

 この集合の包含関係で重要なのは、すべての集合が奇数／偶数によって直和分解できることだ。例えば、\(A\cap C = \{2,4,10,20\}, A\cap C^c =\{1,5\}\)だから、\(A=(A\cap C) + (A\cap C^c) = A\cap(C+C^c) = A\cap U = A（∴ A\subset U)\)である。全体集合Uが、偶数の部分集合Cと奇数の部分集合\(C^c\)に直和分解できることを認識するのが重要である。

さて\((A\cup C)\cap B\)である。直接やっても解けるのだが、\(A\cup C\)が面倒臭い。これは偶数全体に、Aの奇数部分\(A\cap C^c\)を「足した」ものであるから、{1,5}+{2,4,6,....,20}である。これとBの共通部分というのが最終的な答えであるが、Bは３の倍数である。{1,5}に３の倍数は存在しないので、\( C\cap B\)が答えであり、それは偶数の３の倍数であるから{6,12,18}の３つである。したがって、命題(c)は「真」である。

実は、以上の考え方は、論理式の展開の流れをなぞったものになっている。展開すると、
\[ (A\cup C)\cap B = (A\cap B)\cup (C\cap B) = \emptyset \cup (C\cap B) = C\cap B\]となる。

最後の問題は、２つの包含関係式の比較である。左辺は\( (A^c\cap C) \cup B\)、右辺は\( A^c\cap (B \cup C)\)であり、これらが等価かどうか判断せよ、という問題である。論理式を展開してもあまり見通しは良くない感じである。Cと\(C^c\)が任意の集合を２分割するという性質を使えば、\( ... \cap C\)という関係式がある部分をできるだけ生かしたい。

左辺にはこの関係があるので、さっそく適用して見る。\( (A^c \cap C)\)だから、Aに含まれていない偶数の集合であり、それは{6,12,18}+{8,14,16}である。最初の集合はBに含まれている偶数、後者はBに含まれていない偶数である。Bとのunionを最後に考えれば、Bの奇数部分{3,9,15}を足した{6,12,18}+{8,14,16}+{3,9,5}=B+{8,14,16}、つまり３の倍数（20以下）と{8,14,16}が該当する集合となる。

右辺を次に考えてみる。こちらは展開してみると\( A^c \cap (B \cup C) = (A^c \cap B) \cup (A^c \cap C)\)である。AとBは重なりを持たないので、\(A^c \cap B = B\)である。したがって、Bと{6,12,18}+{8,14,16}のunionはB＋{8,14,16}となって、左辺と同じ集合になる。

つまり[ク]の答えは(0)正、正である。 この問題を正しく解く秘訣は、やはり包含関係の図を描くということに尽きると思う。加えて,\(U=C+C^c\)という関係にも注意がいけば、早く解くことができる。