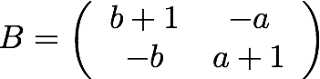円錐曲線の幾何学的な意味：放物線（その１）

二次形式では表せないが、二次関数の代表である放物線の幾何学的な意味を考察してみたい。まず定義から。この定義は、たしか高校の教科書にも載っていたと思う。

y軸上に点Q(0,c)を取る。c＞0と仮定する。

つぎに、y=-cの水平な直線lを考える。

最後に、点Fからの距離と、直線lからの距離が等しくなるような点P(x,y)の集合を考える。

点Qと直線lからの距離が等しい点Pの集合は、
放物線となる。

PQの距離の二乗は（ピタゴラスの定理により）x²+(y-c)²であり、直線lから点Pまでの距離の自乗は(y+c)²である。条件より、これら２つの量（距離の自乗）が等しいとすると、x²+(y-c)²＝(y+c)²が成り立つ。両辺を見比べると、y²がうまく相殺できることがわかる。これにより、yに関しては線形項（つまり1次の項）のみが残ることになる。xに関しては明らかに二次式なので、整理すると

式（１）

すなわち放物線の式（あるいは二次関数の式）を得る。x=0のところで、点Fと直線lからの距離（cとなる）が原点で等しくなるように設定されていることから、この放物線は原点を通ることになった。

c＜0とすると下向きの放物線となる。この証明には、座標をy軸に関してひっくり返すだけでよい。その後で、上の議論を繰り返せば同じ結論を得る。c=0の場合は、直線lと点Fが重なってしまうため放物線にはならない。そもそも、条件を満たすような点Pは原点のみとなり、曲線を描くことはない。この理由によりc=0は除外する。

ここで登場した点Q(0,c)は幾何光学で重要な役割を果たす。この点を「焦点」という。「放物線で反射した光線は必ず焦点に集まる」という幾何学的な意味を持っている。この性質を利用しているのがパラボラアンテナだ。そもそもパラボラ(parabola)というのは「放物線」という意味の英語だ。

焦点の持つこの性質を、計算で確認してみよう。

（つづく）

実対称行列の対角化：二次形式そして円錐曲線との関わり

二次形式という数学の概念がある。二次式というのは二次以下の項を含む多項式のことだが、二次形式というのは二次だけの項からなる多項式のことだ。二次元の場合、自由度はxとyしかないので、二次形式に含まれるのはx², y², そしてxy(=yx)ということになる。これらの線形結合はしたがって、

式（１）

となる。xyの項の係数をわざわざ2bとおいたのは、後できれいな形になるようにしたかったからだ。最初はなにが「きれい」なのかわからないだろうから、単にbと書いておいたって構わない（「２」のご利益については、後でわかるだろう）。

f(x,y)=定数、とおけば、これは二次曲線を表すが、二次形式の場合は円錐曲線、すなわち楕円、放物線、そして双曲線に相当する曲線を表すことになる。たとえば、b=0とし、a>0, c>0と選べば、f(x,y)=定数、は楕円を表すことになる。この間、パンスターズ彗星の軌道が双曲線軌道だという議論をしたが、その議論を深めるには二次形式を学んでおく必要があるというわけだ。

さて、上の二次形式を行列で表現すると次のようになる。

式（２）

真ん中の行列をAで表すとすると、その転置行列はもとの行列に等しいことはすぐに確認できる。つまり, A^t=Aが成り立つ。このような行列を「対称行列」という。a,b,c,dがすべて実数のとき、Aを実対称行列という。（この行列の形をみれば、式（１）で、なぜbではなく、２bとしたかわかるであろう。）

実対称行列が対角化できれば、非常に便利になる。これは、楕円の表現において、長軸短軸（主軸ともいう）にそって座標系をセットするのようなものだ。物理でいう「内部座標」の導入だ。詳細については、別の機会に譲る。

まず確認すべきなのは、「n次の実対称行列は必ず対角化できる」という定理だ。この証明は大学の線形代数の講義でやるが、今は省略し、定理が正しいことを受け入れることにする。

次に必要なのが、実対称行列の固有ベクトル同士は直交し、固有値はすべて実数となる、という定理だ。これは、量子力学で使う「n次のエルミート演算子は対角化可能で、固有値は実数となり、固有ベクトルは互いに直交しあう」という定理の特別な場合に対応する。というのは、エルミート演算子というのはA=A^*tが成り立つ演算子のことをいうが、実対称行列の場合はA=A^*かつA=A^tなので、エルミート演算子に含まれるからだ。（注意：複素対称行列はエルミート演算子ではない。）

ここで二次の正方行列の場合に話を戻し、式（２）で与えられたような実対称行列の固有値と固有ベクトルを求めてみよう。固有値方程式は以前やったように、行列式の形で表すことができる。具体的には、固有値λに対し、|A-λE|=0となる。２次の場合、この行列式はλについての２次方程式であり、実対称行列Aに対しては、

式（３）

となる。ここで、Tr(A)=a+c, det(A)=ac-b²だ。この２次方程式の解は実数になるということが定理で保証されていると上述したが、本当にそうか確かめてみよう。判別式は
D=Tr(A)²-4det(A)
　=(a+c)²-4(ac-b²)
　=(a-c)²+4b²≧0
となって、たしかに実数解をもつことが確かめられる。

２つの固有値を計算すると

式（４）

となる。これに対応する固有ベクトルを計算すると、

式（５）

ただし、N_±は規格化因子で、それぞれ

式（６）

で与えられる。直接計算して確かめることができるが、固有ベクトルは直交している、つまり内積は０(v₊・v_-=0)だ。

前にもやったように、ここで固有（列）ベクトルを並べて、行列Uをつくると、この行列は直交行列になっている、すなわちU^tU=E。（これは実ユニタリー行列と呼ぶこともできる。）この直交性を確かめてみる。まずUは

式（７）

となる。計算してみるとU^tU=Eが成り立つことはすぐにわかる。

ここで、昨日考察した逆行列の問題に行き当たる。つまり、U^tU=EならUU^t=Eが自動的に成り立つかどうか？という疑問だ。昨日の考察を踏まえれば、「成り立つ」ということになるのだが果たしてどうだろうか？計算はかなり面倒になるが、最後までやりきると、ちゃんと成立することが確認できる。

さらに、上の関係式が成り立つということは、U^t=U^-1であることを意味するが、本当にそうなっているだろうか？まず行列式を計算すると（面倒だが）det(U)=-1を得る。これはユニタリー行列の条件|det(U)|²=1を満たしている。

次に、Uの転置行列と、逆行列を形式的に書いてみると

式（８）

と

式（９）

となる。一見したところ、この２つの行列が等しいなんて思いもしないのだが、等しいはずであるから、それを確かめてみよう。全部やるのは大変なので、左上の要素についてここでは確かめてみる。

式（１０）

信じて最後まで計算すれば、ちゃんと等しいことが証明できる！

ということは、一番簡単な表現を使って、

式（１１）

と表すことができるということだ。したがって、Uも簡略化できて、

式（１２）

と書ける。この構造は回転変換の構造とよく似ていることに気付かれたであろう。しかし、回転変換は行列式が１であり、Uの行列式は-1なので、全く同じというわけではない。
これは鏡映反転と関わりがある。例えば、x→-x, y→yという変換Lは

式（１３）

という一次変換で表せる。この辺りの考察はまた後で行うことにしよう。


以上の結果をまとめると、U^tAUが対角行列となり、

式（１４）

このとき、座標系(x',y')は直交変換Uによって(x,y)に移される。すなわち、

式（１５）

この新しい座標系の下では、二次形式はf(x',y')=λ₊x'²+λ_-y'²という形に簡素化される。これは高校で習う円の方程式を含む楕円や双曲線といった円錐曲線の方程式の標準形になっている。つまり、楕円などの円錐曲線を「斜め」からみると、式（１）あるいは式（２）のように非対角項(xyのこと）が生じて、数学的に扱いにくくなってしまうが、うまい座標系へと適当に移ってやれば、簡単な表現へと乗り移ることができるのだ。これは楕円などの円錐曲線を「真っすぐに」みることに対応する。いい座標系を見つけると、問題が簡単になることが多く、楽をして多くの結果を得ることができるのだ。

逆行列の定義

二次形式の考察をしているとき、逆行列の定義が引っかかったので、勉強し直してみた。これが意外にも難しいことがわかった。今まで、逆行列の定義はすんなり受け入れてきたので、ちょっとショックだ。

まずは通常の定義を確認しよう。n次元の正方行列を２つ考え、それぞれをA, Xと書くことにする。単位行列をEとすると、AX=XA=Eが成り立つ時、XをAの逆行列という。（逆に、AはXの逆行列だと言ってもいい。）X=A^-1と表すことが多い。

高校までにおいては２次元の場合しか考察しないが、大学に入ると一般のn次元の場合について考える。その場合の逆行列を与える公式（Cramerの公式ともいう）によると、余因子行列の転置行列に、行列式の逆数をかけたものが、逆行列となる。（余因子については、ここでは説明するのは省略し、別の機会で与えることにする。）この公式から明らかにわかるのは、逆行列の存在は、行列式の逆数が存在するかどうかにかかっているということだ。つまり、行列式が０となる場合には、その逆行列は存在しないということだ。逆行列が存在する時、その行列は「正則である」という（英語ではnon-singularという）。

この条件（つまり逆行列が存在するための条件）は高校でも教わるが、二次元の場合に限られる。二次元の場合の行列式は簡単なので、逆行列が存在するかはすぐにチェックできる。例えば、二次元正方行列Aが

式（１）

で与えられるならば、その行列式det(A)は、

式（２）

となる。この式の幾何学的な解釈については以前議論した。det(A)=0ならAの逆行列は存在しないが、det(A)が０でなければ逆行列A^-1は存在し、

式（３）

となる。

さて、今回気になったのは、AX=Eが成立するのはいいとして、XA=Eが成立することも条件として組み込まなくてはいけないのかどうか？という点だ。逆行列の定義として、かならず「AX=XA=E」と書かれるけれど、AX=Eだけが成立していれば、XA=Eは導出できるのではないか？この問題を書き換えれば、「任意の正方行列Aに対し、AX=Eが成立するXが見つかった時、XA=Eが成立しないようなXは存在するかどうか？」という問題となる。

予想としては、「存在しないんじゃない？」といきたいところだが、果たしてそうなのかどうかは調べてみないといけない。

ちなみに、これに似たような感じの問題が、東大(2007)の第４問に出題されている。

（１）実数aに対し、2次の正方行列A, P, Qが、５つの条件A=aP+(a+1)Q、P² =P, Q²=Q, PQ=O, QP=Oを満たすとする。このとき、(P+Q)A=Aが成り立つことを示せ。

(2),(3)は関係ないので省略。また、この問題自身はとても簡単で、正直に左辺の(P+Q)Aを与えられた条件を利用しながら計算するだけだ。

今、気にしているのは逆行列の定義の方だが、この問題では逆行列の定義自身は直接問われてはいない。が似たような状況が問題で与えられている。それは(P+Q)A=Aなのだが、ここから自動的にP+Q=Eと言えるのかどうかが気になる。もしAに逆行列が存在するならば、自明な結論としてP+Q=Eを得る。しかし、Aに逆行列がないとするならばどうなのだろうか？逆行列が無い場合には、P+Q=EとはならないP+Qが存在して、それが(P+Q)A=Aを満たすというのだろうか？この問題ではAは二次正方行列なので、具体的に書き下して「実験」してみよう。逆行列をもたないAの例として、

式（４）

を考える。P+QをBとおいて、BA=Aを満たすBを求めてみる。すると、答えは一つにはきまらないが、例えば、

式（５）

が条件を満たす。しかし、このBは単位行列とは限らない。(a=b=0の場合のみが単位行列、しかしそのときA=Oとなってしまう。）結論としては、BA=Aだからといって、B=Eかどうかは決定できないということになる。

さて、本題に戻ろう。今度はAB=Eのとき、B=A^-1と言えるかどうか？という問題だ。もしこれが言えれば、自動的にBA=Eは成立する。

両辺の行列式を取ってみると、det(A) det(B)=1となる。この結果、det(A)=0は許されない(同時にdet(B)=0も許されない）ことがわかる。従って、逆行列は存在することになり、BA=Eは自動的に成立する。この証明は一般のn次の場合にも適用できる。

しかし、問題になるのは、Cramerの公式を導くときに、逆行列の定義としてAB=BA=Eを利用したかどうかだ。もし、AB=Eだけで済むのであれば、BA=Eは余分な条件ということになるのだが、この点についてはただいま研究中。だが、ちょっと証明を見た感じでは、どうも利用しているように見える....（卵が先か、鶏が先か？という問題のように見えてきた...）目がまわってきた...

練習問題として、2次正方行列の場合で、正則でない行列Aに対し、AB=Eとなる行列Bを見つけられるかどうか試しに計算してみよう。det(A)=0の例として、上で使ったA（式４）を採用しよう。Bの成分は次のようにおき、Aによってどのように表現できるか計算する。

AB=Eを計算すると、

を得る。結果が０になる式（非対角成分）にまず着目すると、a=0 or q+s=0という条件と、b=0 or p+r=0という条件が要求されることになる。次に結果が１になる式（対角成分）に着目すると、a(p+r)=1とb(q+s)=1だ。最初の２つの条件式から得られるa=0とか、b=0とかいう条件はAに科せられる条件だが、Aは与えられた行列なので自由にいじることはできない。したがって、p+r=0、およびq+s=0の方を選ぶことになるが、これは対角成分より得られた式と矛盾する。つまり、最初の２つの条件式と、最後の２つの条件式を、同時に成立させることは不可能だ。つまり、BがAの逆行列である以外にAB=Eを成立させることはできないということだ。

Aの形を一般形（式１）にして、det(A)=ad-bc=0を付帯条件に課して計算しても、同じ結論になる。

円錐曲線とパンスターズ彗星

パンスターズ彗星が３月１０日に近日点通過し、光度を上げながら、北半球の夕空に姿を見せるようになった。とはいえ、思いの外、暗くて小さな彗星となり、その観測には苦労している人が多いのではないだろうか？私も一週間チャレンジし続け、ようやく昨日撮影することができた。とはいえ、自力ではとうてい発見できなかっただろう。最後は、隣りで観測している人に場所を聞いたのだった...

望遠レンズで撮影した６枚の画像を

gimpを用いて加算合成という方法で画像処理した結果

科学の研究は最初がとても難しい。だから最初にその頂に到達した人を、心の底から褒め讃える習慣がある。ノーベル賞もそのひとつだろう。

さて、天文学科に行くにせよ、宇宙工学を専攻するにせよ、天体／人工衛星の軌道計算に、円錐曲線は欠かせない。

軌道を観測した結果、今回のパンスターズ彗星の離心率は１を越えているという。これは双曲線軌道に対応している。この観測通りであるのなら、パンスターズ彗星は二度と太陽系には戻って来ない。

ちなみに、地球の離心率は0.0167...と極めて０に近い。これは地球の軌道が円軌道（離心率＝０）に非常に近い楕円軌道であることを意味する。ちなみに、火星の軌道の離心率は0.1弱で、地球の離心率よりも一桁大きい。この「大きな」離心率のため（といっても人間の目には円軌道に見えるかも）、ケプラーは火星の軌道計算で非常に苦しむはめになったのだ。

一方、彗星の代表格であるハレー彗星の軌道の離心率は、0.967...と極めて１に近く、その楕円軌道はかなり円形からかけ離れ歪んでいる。離心率が１の円錐曲線は、実は、放物線つまり二次関数だ。ハレー彗星の軌道はむしろ放物線に近いのだ。

以上のように、離心率が１に等しいか、１より大きいか、それとも１より小さいかによって、円錐曲線は３つに分類される。対応する曲線は、順に、放物線、双曲線、そして楕円となる。円は、楕円の特別な場合で、離心率が０の軌道だ。

物理学の観点からすると、高校や中学の数学で、放物線を含むこれらの円錐曲線を一生懸命に学ぶ一つの理由は、重力に従って運動する物体の軌道は必ず円錐曲線のどれかになるからだ。

まずは手始めに放物線の問題からいってみよう。東大理系(2002)の問題。「非常に簡単」と評されている問題だが、彗星の衝突、あるいは彗星と人工衛星をランデブーさせる問題とよみ代えれば、それなりに楽しめるかも。２つの放物線、
y= 2√3 (x - cosθ)² + sinθ
y=-2√3 (x + cosθ)² - sinθ
が与えられていて、これが２点で交わるための、θの条件を求めよというもの。

問題を解くだけなら、連立させてyを消去。xの二次式になるので、判別式を確認して、実数解が２つになる場合を調べればよい。

問題を解く前に、上の放物線の状況について確認しておく。すでに、標準形になっているので、すぐに前者はy=2√3 x²をv=(cosθ,sinθ）方向に平行移動したもの、後者はy=-2√3 x²をv=(-cosθ,-sinθ）方向に移動したものであることがわかる。放物線の極値点は、両者共に単位円(x²+y²=1)の上にあり、２つの放物線は原点に対して点対称の関係にある。これは物理学でいうパリティ変換と同じだから、(x,y) → (-x,-y)という変換に対応する。これは、一次変換であり、かつ角度πの回転変換になっていることはすぐに確認できる。すなわち、

回転変換はユニタリ変換だということは前に見た。実際、行列式は(-1)×(-1)=1となる。三次元のパリティ変換は行列式が-1になるが、二次元の場合は１になる。つまり、二次元のパリティ変換は回転変換と等価で、連続変換（微小回転の繰り返し）で実現できる。一方、三次元のパリティ変換は、回転変換と行列式の正負が異なるため、連続変換（微小回転の繰り返し）では実現できない。

京大(2005)の問題４

京都大学(2005・前期）の問題４。

a³-b³=217を満たす整数の組(a,b)を全て見つけよ。

「１０分で解ける楽勝問題だ！」と思ったが、1×217の場合をうっかり忘れてしまった...このうっかりミス で、本番の入試ならば点数は半減となったことだろう....

因数分解で1×....というのは、自明すぎて頭から抜けてしまいがち。時間を気にして焦るあまり、こういうミスが入試では出てくる。１０分で解けても、２０分は問題を睨んで見落としを無くさないといけない。気をつけるべし。

それにしても、入試問題にはa³±b³系の因数分解がよく出てくる。あまりに慣れ過ぎて、一般の場合が解けなくなるようでも困るし、頭が固まってしまってもまずい。慣れながらも、慣れすぎないという気持ちが大事かも。

ということで、一般化して考えてみることにした。もしかして...と思ってやってみると、案の定うまくいった！ということで、本日「発見」したのが、この恒等式（とはいえ、数百年前に誰かが既に発見しているとは思うが）

式（１）

簡単に証明できるのも嬉しい。符号を＋に変えたバージョンもすぐに証明できるはず。それこそ、「この公式を数学的帰納法で証明せよ」なんて問題がいつかどこかで出るかも。

それにしても、大学入試には意外にも中学で習う数学がかなり出てくるので驚いている。217=7×31という因数分解は中学１年で習う内容だったか？（もしかすると、小学校だったりして。）また、この問題は結局２次方程式を解く事になるわけで、それも中学の問題。つまり、この京大の問題は高校入試レベルの問題ということになるのでは？