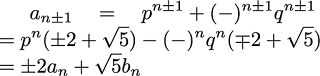いよいよ、この問題の核心である、√7の近似を2/b4でおさえるような有理数近似を見つける作業に入る。具体的には、√7 = a/b + O(2/b4)となるような自然数a,bを見つけることである。
ちなみに、O(n)というのは、n程度の大きさ、ということを意味する数学の記号である。近似理論でよく使われるが、物理の理論は大抵が近似理論なので、よく利用する。テイラー展開なんかも、例えば、Δxの2次で近似する時などは、
f(x+Δx) = f(x)+f'(x)Δx+f''(x)Δx2/2+O(Δx3)
などと書いたりする。
問(1)で、a,bの代わりに自然数m,nを使う表現に問題を書き直した。a=2n+m, b=nとすると、問題で与えられた不等式(1)は
|m/n - δ| < 2/n4 (B)
となる。δは、δ=√7 - 2で定義され、
0.645 < δ < 0.646
を満たす。 近似式を利用すると√7 = 2 + (m/n) + O(2/n4)となるので、m/nは√7の小数部分δの有理数近似に対応する。つまり、
δ= m/n + O(2/n4)
ということである。小数部分だから
m < n
という制限がつく。これを満たすm,nを見つけるには、書き換えた不等式(B)をm,nに関する条件式とみなす。このとき、m/n - δ の正負の応じて場合分けして考える。
[1] m/n > δの場合:
これはよく「上からおさえる近似」と呼ばれる。つまり、近似したい量よりも「上側」つまり大きい量で近似する、というやり方である。絶対値の記号を外すと m/n - δ < 2/n4 となる。δに関して整理すると m/n - 2/n4 < δ < 0.646となる。不等式の最後は、δの範囲を与える条件式の適用である。0.646を有理数、つまり整数の商の形で表すと 0.646 = 323/500 = 323/(5322)である。両辺に分母にある5322とn4 をかけて、整数の和積の形に書き直すと、不等式(B)は
(5322 m-323n)n3 < (5・2)3
という不等式に書き換えることができる。ちなみに、右辺をうまい具合に3次式でまとめることができたのは、誤差2/n4の係数2のおかげである。どうしてもっとスッキリした1/n4という形にしなかったのか?という疑問はここで解決される。
さて、このままでは、問題を解く緒は得られないが、3乗の因子が2つ出てきたので、これをまとめてみる。すると
(5322 m-323n) < (10/n)3 (B')
となる。この不等式の左辺は自然数の積和(積差)になっているから、当然自然数である。一方、右辺に関してはn>10のとき、1より小さい数になる。1より小さな自然数は存在しないから、このとき上の不等式を満たすn,mは存在しないことになる。したがって、n≦10でなくてはならない!
この方法だと、結構たくさん調べなくてはならないが、「近似」という観点から問題を解いているので、頭で何をやっているのか理解しやすい。AIならば、意味もわからず、すべての組み合わせについて調べ上げるだろう。これがAIと人間の違いである。とはいえ、n≦10の検算に関しては、我々はAIになったつもりで計算しなくてはならない...というか、普通はコンピュータや電卓に頼って計算を進めることになる。
すべての計算を網羅したら飽きてしまうので、ここでは具体例を2、3絞ってやってみよう。
(1) n=2の場合。n=2を(B')式に代入すると、500m - 646 < 125となる。m< nなのでm=1しか選択肢がない。左辺=-146となって条件は満たされない。n=2は除外される。
(2) n=3の場合。m=2,1の2つのケースを試すことができる。(B')式は 500m - 969 < (1000/27)=37.03...となる。m=1の場合は、左辺が負になるからダメ。m=2のときは、1000-969 = 31となり、37より小さい値になる。つまり、この時、条件は満たされる。
a=2×3 + 2 = 8, b= 3、つまり8/3は問(2)の答えであり、√7のよい近似になっている。√7 = 8/3 + O(0.01)である。O(0.01)は、2/34=0.02469...を意味する。
(3) n=4の場合。(B')式は500m - 1292 < (125/8) = 15.6...となる。m=3,2,1が試せるが、n=2,1の場合は左辺は負になるのでダメ。m=3を代入すると1500-1292 = 208となってダメ。
ここまでの検算でわかるのは、右辺の量 (10/n)3 はnが増大するにつれて1に近づく。これは誤差の許容範囲が狭くなるという意味があり、近似の観点からするとよいのだが、あまりに厳しすぎると、この条件をクリアーできる自然数が見つからない、というジレンマが生まれる。上の計算のn=3では右辺が37程度と大きかったのだが、n=4では15程度に半減している。もちろん、n=4の場合は左辺が208ととても大きくなってしまったので、たとえ右辺が37程度であったとしてもダメだったわけだが。
こうなると、負になる場所を見極めておいた方が計算が楽になることが予想される。
500m - 323 n > 0とすると、m/n > 323/500 = 0.646となる。つまり、nの大きさよりも60%以上大きな値をmが取る場合だけが有効なケースである。n>mだから mの最大値はn-1で、これはm/n=(n-1)/nである。したがって、1-(1/n) > 323/ 500を解くと、
n > 500/177= 2.88..となるので、n≧3においてはm=n-1の計算をしても右辺が負になることはない。次に、m=n-2の場合を調べてみよう。n=3,4の場合では左辺は負になってしまった。m/n= (n-2)/n > 323/500を解くと、n> 2(500/177) = 2×2.88 = 5.76となり、6より大きな数でないと負になることがわかった。
m=n-kが左辺の量を正に保つには n> k(500/177) = 2.88kという条件が一般になりたつことがわかる。nが大きくなれば、選択肢が増えて答えがたくさんみつかりそうな気がするが、そうは問屋が卸さない。左辺の量はmの1次関数とみなすことができ、その増加率はmの係数(「傾き」に相当する)500で与えられる。つまり、mが1ずれるごとに、左辺の量は500もずれてしまう。nが大きくなると、逆に右辺は減少して1に近づいていく。つまり、左辺が500も動くのでは、精度が1程度の近似が要求された場合には、2つも3つも適合する自然数が存在するわけがない。つまりチャンスはk=n/2.88で与えられるm=n-k付近の一回ぐらいしかないとみてよい。
いずれにせよ、n=5,6,7,8,9,10の場合を試しても、要求された精度を満たすmは存在しないことが確認できる。したがって、(n,m)=(3,2)だけがこの場合の答えである。
[2] m/n < δの場合:
この場合は、(B)式で絶対値の記号を外すと、(2/n4)+(m/n) > δ > 0.645=129/200となる。この式も、分数を消してまとめることにする。今回は
( 129n- 200m )n3 < 2452
となってしま、うまい具合に3乗の形で右辺をまとめることが、そのままではできない。[1]m/n<δの場合と同じような形にするには、両辺に22・5をかけるとよい。すると
2580n - 4000m < (20/n)3
という形にすることができる。したがって、今回はn≦20の場合について検算する。数が大きくなって、計算は[1]の場合よりも大変になる。試験場に電卓を持ち込みたくなるだろう。が、我々は試験会場にはいないので、電卓を使って、ちゃちゃっと計算してしまうと、実は条件を満たすm,nの組みは存在しないという結論になる。
以上、[1][2]の結果をまとめると、問(2)の答えは一つだけで、8/3という、案外平凡な答えになる。上で展開した面倒臭い議論なんかすっとばして、直感でやっても辿り着けそうな答えである。どうせなら、123457/ 46663 みたいな、とんでもない大きな素数の商なんかに答えがなっていたら、もっと楽しかったのだが....
この問題を上のようにして解いてみてわかったのだが、有理数近似の精度は2/n4という誤差の形式にもよるが、案外0.645<δ<0.646という、δの範囲の精度にも依ることがわかった。したがって、より精度の高い有理数を探したいとおもったら、この不等式の精度をあげないといけないのだろう。√7=2.64575...だから0.6457<δ<0.6458としたら、どんな有理数で近似できるのだろうか?やってみたら案外面白いかもしれない。
2017年3月13日月曜日
2017年3月12日日曜日
阪大2次試験(2017) 問題(3): その0
まず、この問題は√7が無理数であることから考えを始める必要がある。無理数と有理数の違いは、整数m, nの商によって表現できるか、できないかの違いである。つまり、有理数はm/nと表せる数なのに対し、無理数はそのようには表せないのである。√7は無理数だと問題で言っているので、√7 = m/nとなるようなm,nを見つけることはできない。
にもかかわらず、√7をm/nで(つまり有理数で)近似したい、というのが不等式(1)の意味である。こういうことは、電子計算機(つまりコンピュータ)のような限られたビット数で無理数を表現(近似)するときに必要とされる。物理学者は、円周率πやネイピア数eなど、無理数で記述される色々な自然現象を、計算機でシミュレーションするので、できる限り良い精度で無理数を有理数近似する方法には、興味があるのだ。
(1)式の右辺は√7と2つの自然数の商a/bの差である。このような差のことを誤差という。誤差が小さければ、a/bは√7の良い近似になっているといえる。
この問題で「誤差が小さい」というのは、右辺の2/b4で表現されている。関数y=4/x4は単調減少のグラフであり、x>1の領域でxが増大すると急速に減衰(damp)する。bは2以上の自然数だから、2/b4は1/8より小さい値を持つ。つまり、不等式(1)の意味は、「√7を有理数a/bで近似した時の誤差が、最大でも1/8程度で抑えられるような場合」となる。
次に、√7の値が2以上、3以下であることから、a>bでなくてはならないことがわかる。もしa=3bであるならば、a/b=3であるから、問題文で与えられた、√7の大きさを示す不等式から 0.354 < 3-√7 < 0.355が得られる。1/8=0.125だから、√7を3で近似するのはちょっと粗すぎる、ということになり、a/b=3という試みは不等式(1)を満たさないことになる。今度はa/b=2としてみる。すると 0.645 < √7 - 2 < 0.646、つまり|√7 -2| < 0.646となって、精度はもっと悪くなってしまう。
ここで、誤差の意味合いをはっきりさせるために、δ=√7 - 2という量を導入しよう。これは√7の少数部分の大きさを意味する。無理数なので、少数表記すると無限に続いてしまうような量であり、当然自然数や整数の商(比)によって表すことができない量である。ただ、問題文により、δの大きさには上限、下限が与えられており、それは
0.645 < δ < 0.646
である。
今度はa/bの方を2+ε,ただし0 < ε < 1、と表すことにする。a/bは有理数だから、εは何らかの自然数m,n によってε=m/nと書くことができる。つまり、
a/b = 2 + ε = 2 + m/n = (2n+m)/n
すなわち、a= 2n+m, b=n, m < n, と表すことができる。
従って、与えられた不等式(1)は、a/b - √7 = m/n - δなので
|ε - δ| < 2/n4 ≦ 1/8
と書き直すことができる。
また、証明すべき式は a/b + √7 = (2+ε) + (2+δ) = 4 + ε + δ、なので|4+ε+δ| < 6となるが、今、ε>0, δ> 0.645>0なのでε+δは正の量。したがって、 不等式は4 + ε + δ < 6と書けて、
ε+δ < 2
を示せばよいことになる。
さらにδ< 0.646なので、ε=m/n < 1〜1.2 あたりの不等式が示せれば、ε+δ< 0.646 +1< 2となって証明終わりというわけだ。
δは√7の少数部分であるから当然1よりは小さい。εは√7の少数部分の有理数近似だから、δと同じ程度の大きさになっていてほしい量。両者共に1以下の正の量だとすれば、その和は2より小さくなるでしょ、というのが上の不等式の意味で、これはある意味当たり前の話だ。
数学の問題としては、「εの近似の精度が(1)で与えられているときに、当たり前のことをきちんと証明してみなさい」ということなんだと思う。大学に入ると、εδ法というのを習って、実数の連続性とか、収束の概念なんかを習う。極限の具体的な計算法を知っているのに、計算などは一切やらず、その手前の話を延々とやっているように感じて、気が遠くなった。ひどいときには、足し算の証明なんかを、アルキメデスの公理から出発して議論したりした。足し算の有効性についての証明が終わった後、「来週は割り算をやります」とか先生が言った瞬間、「小学校か、ここは...」と絶句した記憶がある。
しかし、計算式や公式を鵜呑みにして「当たり前」に計算していたことを改めて考えたりするのは、実は理論研究をやる上で、とても大切なアプローチだ。研究で、誰もやっていないところに進むときは、基礎から固めていかなければならないので、ああいう基礎的な考え方が意外に必要になるのだ。割り算や足し算の本当の意味は、もっと進んだように見える理論で、思いもかけず似たような形で再登場するのかもしれない。残念ながら、多くの学生は、こういう議論の意図がわからず脱落していく。真実を極めるタイプの研究には、こういう基礎的な考察は必須である。
さて、問題に戻るとする。条件式(1)においてε>δになるようにmを調整すると
ε+ δ = (ε-δ) + 2δだから、
ε+δ < ε-δ + 2×0.646 = ε-δ + 1.292 < 1/8 + 1.292 = 1.417 < 2
となって証明終わり。証明すべき不等式は、実はかなりの「ザル勘定」で上限を抑えていることがわかる。つまり、(1)を満たす√7の有理数近似a/b=(2n+m)/nの精度はそれほどよいというわけではないということだ。
一方で、mの調整がどうしてもうまくいかず、ε < δとなってしまったとする。このときは、ε+δ = |-ε-δ| = |δ-ε-2δ|なので
0 > -δ-ε = (δ-ε) - 2δ > (δ-ε) -2×0.646 > (δ-ε) - 1.292 > -1/8 - 1.292 = -1.417 > -2
となり、同じように証明できた。
2017年3月10日金曜日
東大2次試験(2017): 問題5 ( 感想 )
x⇄yという交換に対する対称性があると、やはり色々なところが綺麗になる。この考え方を貫けなかったので、k < -3/4における解の分類を直感的に行うことができなかったのは反省点である。たすき掛けの解ひとつひとつは対称性を破る。しかし、2つをペアとして考えると、対称性は「回復」される。一方で、蛾の羽の先端解は、もともとの対称性を受け継いだ解となっている。
物理学では、もともと後者の解、つまりもともとの対称性(たとえば、ハミルトニアンやラグランジアンの持つ対称性)を受け継いだ解だけしか考えなかった。ところが、この対称性を破るような解も存在することに20世紀の中頃以降の物理学者たちは気がついた。その端緒を切ったのが、南部先生の提唱した「自発的対称性の破れ」であり、それを回復させる「南部ゴールドストーンモード」である。
実は、これと同じようなことは相転移の物理でも起きていて、例えば磁性体の相転移では、臨界温度以下で自発的に(回転)対称性が破れ、一方方向に磁化がそろう(つまり、電子スピンの磁気モーメントが揃う)ような状態に変遷する。
この問題では、温度に対応する制御パラメータkを通して、系の持つ対称性を尊重した解(蛾の羽の先端解および、たすき掛けの縮退した解)から、対称性の破れた解 (たすき掛けの解)へと「相転移」するシミュレーションモデルになっている、などと考えることができれば、なかなか楽しめるのではないだろうか?特に、kの値に応じて、共通接線を表現する接点の位置x0を与える3次関数f(x)の形状がどのように変わるか調べるのは、理論物理学者にとってはよく習熟しておくべき、「基礎的な技能」であろう。
物理学では、もともと後者の解、つまりもともとの対称性(たとえば、ハミルトニアンやラグランジアンの持つ対称性)を受け継いだ解だけしか考えなかった。ところが、この対称性を破るような解も存在することに20世紀の中頃以降の物理学者たちは気がついた。その端緒を切ったのが、南部先生の提唱した「自発的対称性の破れ」であり、それを回復させる「南部ゴールドストーンモード」である。
実は、これと同じようなことは相転移の物理でも起きていて、例えば磁性体の相転移では、臨界温度以下で自発的に(回転)対称性が破れ、一方方向に磁化がそろう(つまり、電子スピンの磁気モーメントが揃う)ような状態に変遷する。
この問題では、温度に対応する制御パラメータkを通して、系の持つ対称性を尊重した解(蛾の羽の先端解および、たすき掛けの縮退した解)から、対称性の破れた解 (たすき掛けの解)へと「相転移」するシミュレーションモデルになっている、などと考えることができれば、なかなか楽しめるのではないだろうか?特に、kの値に応じて、共通接線を表現する接点の位置x0を与える3次関数f(x)の形状がどのように変わるか調べるのは、理論物理学者にとってはよく習熟しておくべき、「基礎的な技能」であろう。
2017年3月9日木曜日
東大2次試験(2017): 問題5(その4)
さて、一応答えは出たので、この辺で終了にしてもよいのだが、我々の目的は単なる試験問題の解説ではない。そもそも、試験を解くだけなら、あんな面倒な方法でやらなくったって、巷に溢れる「優秀な解答」のように短い計算でちゃちゃっとやってしまえばよいのである。しかし、答えを得るだけでは、問題の本質は理解できないし、問題の一番楽しいところも素通りだ。とはいえ、たまたま見つかった特別な因数分解を頼りに問題を解き進めるのは、いくらなんでも、ちょっと不安になるだろう。
そこで、付録として、もう少し一般の場合でも解けるように、「普通」の方法でこの問題(3次方程式の解の分類)を解いてみよう。
この方法では、極値の位置の分類によって、解の個数を調べる。そのためには3次関数の微分を計算し、極値の位置を調べる必要がある。一般に極値はdf(x)/dx=0を解いて与えられ、この問題では2次方程式として表される。すなわち
である。この方程式の判別式はD=4k2+3k=k(4k+3)であり、またもやk=-3/4が登場する。気をつけるべきは、この判別式は「極値の数」を判別するものであって、共通接線の数を判別した前回の判別式とは異なる役割をもっているという点だ。
D<0のとき実数解は存在しない。すなわち極値は存在しない。この状況に対応するのは-3/4 < k < 0のときで、このとき3次関数f(x)は極値を持たず、単に変曲点がx0=2k/3にあるだけだ。したがって、単調増加のグラフとなる。この領域では共通接線の数は1つだけである。
前回の分析との関わり合いを見てみる。-1/2 < 2k/3 < 0なので、常に存在する「蛾の羽の先端解」の接点x0=-1/2に対し、その右側に変曲点はある。また、この変曲点における3次関数の値はf(2k/3)=(1+4k/3)(1-4k/3)となり、これは-3/4<k<0の領域で正値をとる。つまり、f(2k/3)>0である。この領域(-3/4 < k < 0)で単調増加なグラフが、x → -∞において、f(x) → -∞であるし、f(2k/3)>0であれば、その間に解が一つあるのは明らかだ。そして、詳しい計算をすれば、それはx0=-1/2 (< 2k/3)になるはずである。
D=0となるのはk=-3/4とk=0の場合である。k=0の場合は、f(x0)=8x03+1=(2x0+1)(4x02-2x0+1)となる。2つ目の因数4x02-2x0+1は常に正(判別式は1-4=-3<0)であるから、接点は一つしかない(蛾の羽の先端解に対応するx0=-1/2)。実際はk < 1/4の領域では解の数は一つであるから、この結果は当然の結果であるが、0 < k < 1/4の領域でも解が一つしかないことを示すためには、極大値の位置を調べる必要がある。
極値の分析を始める前に、もう一つやれることがある。それはまたもや対称性に関連する分析である。上のグラフを見てみるとわかるように、0<k<1/4においては、放物線CとDが交点を持ってしまい、重なってしまうので「たすきがけ」ができない。これが、k=0の場合以外でもそうかどうか、CとDの交点について調べてみよう。CとDの方程式を連立してみると、x4+2kx2-x+k2+k=0 となって4次方程式である。判別式かなにかでCとDの交点の数を数えられるかと思ったが、これはちょっと厄介である。
ちなみに、k=0ならばx4-x=x(x3-1)=x(x-1)(x2+x+1)=0となる。最後の因子に対応する2次式の判別式は負になるから実数解を持たない。解はx=0,1となって上の図の通りである。しかし、これではどのkの値のときに交点が発生するかよくわからない。
よく図を見ると、CとDの交点は、y=xとの交点にもなっていることがわかる。これはひとえに対称性のなせる技だ。つまり、CとDの連立方程式である4次方程式を解かなくとも、Cとy=xの連立方程式、それは2次方程式、を研究すれば、交点の数は分析できるのである。そしてそれはすでに最初に分析済みである。連立した結果の2次方程式はx2-x+k=0であり、その判別式はD=1-4kである。つまり、k<1/4のとき、CとDは交点を2つ持つ。k=1/4の時は接するので1つ。そして、k>1/4で交点は0である。つまり、「たすき掛けの解 」は、CとDの間に隙間があかなくては発生しないのである。
極値の議論に戻ろう。極値の有無を判別する2次式の判別式が零値をとる場合として、
第二臨界値であるk= -3/4がある。この場合、共通接線3本は一本に縮退し、a=-1の解、つまり蛾の羽の先端解に収束する。
したがって、3次関数の極値が2つ(つまり極小値と極大値がひとつずつ)が、「しっかり」生じる可能性があるのはk < -3/4、またはk>0の領域ということになる。極値の位置は上の2次方程式の解で得ることができ、
である。正符号(+)は極小点、負符号(-)は極大点に相当する。 この値を3次式f(x)に代入すれば極値が得られる。ただ、解を3乗したり2乗する計算はそれなりに手間がかかる。そこで、手間を省くために、2次方程式を変形してx02=(4kx0+k)/3とし、これを3次関数に代入することで計算を簡単にすることができる。変形の結果はf(x0)=-(16/9)k(4k+3)x0-(16/9)k2+1となり、線形になる。ここにx0±を代入し計算すれば、極値が得られる。
極値の値は、予想通り「面倒臭い」形になる。
この式は、しかしながら、意外にも比較的綺麗な形へと変形できるのである。まずは、平方根を含まない、最初の3項を考えよう。係数を分母と分子のそれぞれで因数分解すると
となって、うまい具合に4/3でまとめることができる。しかもその係数は-2, -3, +1であるから、k=-3/4を代入すると、綺麗に0となる。つまり因数定理により、この多項式は因数分解できて-(1/27)(4k+3)2(8k-3)となる。この結果と平方根の項をまとめると、
となる。
解が3つ存在するためには、極大値が正値をとり、極小値が負値をとる必要がある。すなわち、条件式としてはf(x0-) > 0, かつf(x0+) < 0となる。
まずは、k< -3/4の場合を考えてみよう。といっても、結論は k < -3/4になるわけだから、上の条件式はこの領域で常に成り立ってしまうはずである。実際、-(16/27)(4k+3) > 0なので、条件式は
となる。4k+3 < 0, 8k-3 < 0, k<0なので、2つ目の不等式はこの領域で常に成り立つことはすぐにわかる。一方、上の式は第二項を右辺に移行する。両辺は正の量なので、自乗してもよい。負の量4k+3で両辺を割ると不等号の向きが変わることに注意すると 4^4*k^3 - (4k+3)(8k-3)2 < 0となる。左辺を計算して整理すると27(4k-1) < 0となる。この条件式も常に成り立つ。したがって、上の不等式はk < -3/4の領域で「恒等不等式」になっていて、つまらない分析ではあったが、新しい条件が出てこないことが確認できた。つまり、k < -3/4では、共通接線は3つあるということである。
次に、k>0の場合を考えよう。今度は-(16/27)(4k+3) < 0なので、上の不等式の向きは両方ともひっくりかえる。そして、8k-3の正負によって計算が変わってくる。まずは8k-3>0つまりk>3/8の場合を考えよう。このとき、一番上の不等式は恒等的に成り立つから、これ以上の分析は不要。一方、2つ目の不等式は第二項を右辺に移行してから自乗する。両辺正の量だから不等号の向きは変わらない。両辺を4k+3>0で割っても、符号の向きは変わらないから、不等号の向きが逆転する以外は、上の考察の場合とほぼ同じになって27(4k-1)>0となる。しかし、もともとk>3/8 (> 1/4)の場合を考えていたので、まとめるとk > 3/8になる。一方、8k-3 < 0の場合、2つ目の不等式は恒等的に成り立つのに対し、最初の不等式については初項を右辺に移行してから自乗し、4k+3(>0)で両辺を割る。その結果は27(4k-1) > 0となる。k>0, 8k-3<0の結果と合わせると、1/4 < k < 3/8となる。以上の分析をまとめると、k>0の場合、共通接線が3つ存在するのは 1/4 < kの領域である。
ここまでの分析でわかったのは、
k < -3/4 の場合、共通接線は3つ。
-3/4 < k < 0 の場合、共通接線は1つ。
k > 1/4 の場合、共通接線は3つ。
である。
やり残したのは、2つの臨界点(k=-3/4, 1/4)における考察と、0 < k < 1/4において、共通接線が1つしかないことの証明だが、これらも極値の位置関係を調べることで、答えが得られる。
最後に、3次関数y=f(x)が、パラメータkに対し、どのように振る舞いを変えていくかを、解の個数の観点から図にまとめてみた。 左上から、時計回りにkが減少していくように配置した。
そこで、付録として、もう少し一般の場合でも解けるように、「普通」の方法でこの問題(3次方程式の解の分類)を解いてみよう。
この方法では、極値の位置の分類によって、解の個数を調べる。そのためには3次関数の微分を計算し、極値の位置を調べる必要がある。一般に極値はdf(x)/dx=0を解いて与えられ、この問題では2次方程式として表される。すなわち
である。この方程式の判別式はD=4k2+3k=k(4k+3)であり、またもやk=-3/4が登場する。気をつけるべきは、この判別式は「極値の数」を判別するものであって、共通接線の数を判別した前回の判別式とは異なる役割をもっているという点だ。
D<0のとき実数解は存在しない。すなわち極値は存在しない。この状況に対応するのは-3/4 < k < 0のときで、このとき3次関数f(x)は極値を持たず、単に変曲点がx0=2k/3にあるだけだ。したがって、単調増加のグラフとなる。この領域では共通接線の数は1つだけである。
前回の分析との関わり合いを見てみる。-1/2 < 2k/3 < 0なので、常に存在する「蛾の羽の先端解」の接点x0=-1/2に対し、その右側に変曲点はある。また、この変曲点における3次関数の値はf(2k/3)=(1+4k/3)(1-4k/3)となり、これは-3/4<k<0の領域で正値をとる。つまり、f(2k/3)>0である。この領域(-3/4 < k < 0)で単調増加なグラフが、x → -∞において、f(x) → -∞であるし、f(2k/3)>0であれば、その間に解が一つあるのは明らかだ。そして、詳しい計算をすれば、それはx0=-1/2 (< 2k/3)になるはずである。
D=0となるのはk=-3/4とk=0の場合である。k=0の場合は、f(x0)=8x03+1=(2x0+1)(4x02-2x0+1)となる。2つ目の因数4x02-2x0+1は常に正(判別式は1-4=-3<0)であるから、接点は一つしかない(蛾の羽の先端解に対応するx0=-1/2)。実際はk < 1/4の領域では解の数は一つであるから、この結果は当然の結果であるが、0 < k < 1/4の領域でも解が一つしかないことを示すためには、極大値の位置を調べる必要がある。
 |
| k=0の場合 |
ちなみに、k=0ならばx4-x=x(x3-1)=x(x-1)(x2+x+1)=0となる。最後の因子に対応する2次式の判別式は負になるから実数解を持たない。解はx=0,1となって上の図の通りである。しかし、これではどのkの値のときに交点が発生するかよくわからない。
よく図を見ると、CとDの交点は、y=xとの交点にもなっていることがわかる。これはひとえに対称性のなせる技だ。つまり、CとDの連立方程式である4次方程式を解かなくとも、Cとy=xの連立方程式、それは2次方程式、を研究すれば、交点の数は分析できるのである。そしてそれはすでに最初に分析済みである。連立した結果の2次方程式はx2-x+k=0であり、その判別式はD=1-4kである。つまり、k<1/4のとき、CとDは交点を2つ持つ。k=1/4の時は接するので1つ。そして、k>1/4で交点は0である。つまり、「たすき掛けの解 」は、CとDの間に隙間があかなくては発生しないのである。
極値の議論に戻ろう。極値の有無を判別する2次式の判別式が零値をとる場合として、
第二臨界値であるk= -3/4がある。この場合、共通接線3本は一本に縮退し、a=-1の解、つまり蛾の羽の先端解に収束する。
したがって、3次関数の極値が2つ(つまり極小値と極大値がひとつずつ)が、「しっかり」生じる可能性があるのはk < -3/4、またはk>0の領域ということになる。極値の位置は上の2次方程式の解で得ることができ、
である。正符号(+)は極小点、負符号(-)は極大点に相当する。 この値を3次式f(x)に代入すれば極値が得られる。ただ、解を3乗したり2乗する計算はそれなりに手間がかかる。そこで、手間を省くために、2次方程式を変形してx02=(4kx0+k)/3とし、これを3次関数に代入することで計算を簡単にすることができる。変形の結果はf(x0)=-(16/9)k(4k+3)x0-(16/9)k2+1となり、線形になる。ここにx0±を代入し計算すれば、極値が得られる。
極値の値は、予想通り「面倒臭い」形になる。
この式は、しかしながら、意外にも比較的綺麗な形へと変形できるのである。まずは、平方根を含まない、最初の3項を考えよう。係数を分母と分子のそれぞれで因数分解すると
となって、うまい具合に4/3でまとめることができる。しかもその係数は-2, -3, +1であるから、k=-3/4を代入すると、綺麗に0となる。つまり因数定理により、この多項式は因数分解できて-(1/27)(4k+3)2(8k-3)となる。この結果と平方根の項をまとめると、
となる。
解が3つ存在するためには、極大値が正値をとり、極小値が負値をとる必要がある。すなわち、条件式としてはf(x0-) > 0, かつf(x0+) < 0となる。
まずは、k< -3/4の場合を考えてみよう。といっても、結論は k < -3/4になるわけだから、上の条件式はこの領域で常に成り立ってしまうはずである。実際、-(16/27)(4k+3) > 0なので、条件式は
となる。4k+3 < 0, 8k-3 < 0, k<0なので、2つ目の不等式はこの領域で常に成り立つことはすぐにわかる。一方、上の式は第二項を右辺に移行する。両辺は正の量なので、自乗してもよい。負の量4k+3で両辺を割ると不等号の向きが変わることに注意すると 4^4*k^3 - (4k+3)(8k-3)2 < 0となる。左辺を計算して整理すると27(4k-1) < 0となる。この条件式も常に成り立つ。したがって、上の不等式はk < -3/4の領域で「恒等不等式」になっていて、つまらない分析ではあったが、新しい条件が出てこないことが確認できた。つまり、k < -3/4では、共通接線は3つあるということである。
次に、k>0の場合を考えよう。今度は-(16/27)(4k+3) < 0なので、上の不等式の向きは両方ともひっくりかえる。そして、8k-3の正負によって計算が変わってくる。まずは8k-3>0つまりk>3/8の場合を考えよう。このとき、一番上の不等式は恒等的に成り立つから、これ以上の分析は不要。一方、2つ目の不等式は第二項を右辺に移行してから自乗する。両辺正の量だから不等号の向きは変わらない。両辺を4k+3>0で割っても、符号の向きは変わらないから、不等号の向きが逆転する以外は、上の考察の場合とほぼ同じになって27(4k-1)>0となる。しかし、もともとk>3/8 (> 1/4)の場合を考えていたので、まとめるとk > 3/8になる。一方、8k-3 < 0の場合、2つ目の不等式は恒等的に成り立つのに対し、最初の不等式については初項を右辺に移行してから自乗し、4k+3(>0)で両辺を割る。その結果は27(4k-1) > 0となる。k>0, 8k-3<0の結果と合わせると、1/4 < k < 3/8となる。以上の分析をまとめると、k>0の場合、共通接線が3つ存在するのは 1/4 < kの領域である。
ここまでの分析でわかったのは、
k < -3/4 の場合、共通接線は3つ。
-3/4 < k < 0 の場合、共通接線は1つ。
k > 1/4 の場合、共通接線は3つ。
である。
やり残したのは、2つの臨界点(k=-3/4, 1/4)における考察と、0 < k < 1/4において、共通接線が1つしかないことの証明だが、これらも極値の位置関係を調べることで、答えが得られる。
最後に、3次関数y=f(x)が、パラメータkに対し、どのように振る舞いを変えていくかを、解の個数の観点から図にまとめてみた。 左上から、時計回りにkが減少していくように配置した。
 |
| 赤い丸に対応するのが、「蛾の羽の先端解」で、x=-1/2に相当する。この解は、どの場合にも存在していることがわかる。各グラフの左上の数字は、解の個数、すなわち共通接線の個数を表す。 |
2017年3月8日水曜日
東大2次試験(2017): 問題5(その3)
問(2)の続き。
確認のため、3次関数をもう一度書くと、
となる。
今回は、対称性の考察からx0 = -1/2という解を幸運にも見つけ出すことができた。因数分解により、残りの2つの解は2次方程式を解いて得ることができる。実数解の条件である判別式が正の場合(D=(4k+3)(4k-1) > 0)、 つまり k < -3/4、あるいはk > 1/4において、残る2つのの接点のx座標は
と計算される。
a=2x0、b=x02+k = 2(k + 1/4)x0 + k - 1/4を使って共通接線を引いてみると、「たすきがけの解」の意味あいがはっきりする。例によってpostscript言語によって図を描画してみると次のようになる。まずはわかりやすいk=1( > 1/4)の場合から。
図を見ると、どうも「たすき掛けの解」はy=xに関して線対称になっているように見える。この点については後ほど議論する。
次はいよいよk=-2 (< -3/4)の場合だ。「蛾の羽の先端解」以外の解が、果たして「たすき掛けの解」に似たようなものになっているのか、それとも全く異なる想像を絶するようなものなのか?
結局、「たすき掛け」によく似た形になっているのがわかる(青線、緑線に対応)。世の中、想像を絶するようなことはそうそう起こらないものだ。それぞれの接線は、y=xに対して線対称の関係にあるように見える。放物線と放物線の間の領域が「閉じて」しまったため、いわば、共通接線は、「蛾の羽の先端」をかすめつつ、蛾の止まる「葉の縁」へと接している。「葉の縁」に接するかどうかは、なかなか直感では判断つきにくい。そうかもしれないが、そうじゃないかもしれない、と疑いはもてるものの、断定できない。数式はそこを「無機質に」ではあるが、断定してくれるので、ありがたい。
k < -3/4の領域でどのように3本の共通接線が存在できるのか、直感的な理解はできた。しかし、第二臨界点であるk= -3/4では、たった1本だった共通接線が、k < -3/4の領域に入った途端、突然3本に増加するという、このメカニズムは、いまだに理解しがたいものがある。なんとなく、蛾の羽の先端が開くとき、一気に縮退が解ける感じは想像できるのだが、図をつかってその様子を明らかにしておこう。
臨界点からわずかにずれた、k= -3.001/4.0 あたりを見てみよう。
この図からわかったのは、対称性の縛りが、どうしても3本の共通接線を作り出している、ということである。k= -3/4の縮退は y=xと線対称な直線y=-x+bへの縮退であった。このとき、y=-x+bに線対称な直線は自分自身である。これが縮退の正体である。ところが、若干でも臨界状態からずれたとたん、縮退がほどけた接線のうち、線対称でなくなった直線(例えば緑線)は、その直線に線対称な直線(青線)の存在を許すことになる。こうして、一本だった共通接線は第二臨界点を界に突然3本に増えるのである。
第一臨界点(k= 1/4)での縮退の正体は、共通接線が対称線y=xに重なるというものだった。たしかにy=xはy=xに対して「線対称」ではあるが、y=xとは直交してない。このため、縮退が解けても、線対称の関係にある青線と緑線の2本しか発生しなかったのである。直交する共通接線、つまり蛾の羽の先端解はひとり別のところ(x0=-1/2)で、y=xに直交する共通接線を作っていたのである。
さて、この辺りで試験問題の解答も解いておこう。a=2の場合である。問(1)ではb, kをaで表現したので、それを使えばよい。が、あの表式はa≠ -1, 0という縛りがあったのを忘れるべからず。とりあえず、a=2の計算はできるので計算すると、k = 3/8を得る。また、b = -5/8である。
今まで見た来たように、この問題でもっとも重要なのはパラメーターkである。k=3/8というのは第一臨界点k=1/4の上部、すなわち 3/8 > 1/4にある。この領域で、共通接線の数は3本あることを我々はすでに知っている。また、この時「蛾の羽の先端解」と「a=2に線対称な解」があることも我々はすでに知っている。蛾の羽の先端解の場合、傾きは常にa=-1である。接点はもう何度も出て来たようにx0=-1/2である。ここで導いた関係式b = -x02+kを使ってb=1/8が得られる。対称解は、すでに得られた答えy=2x-5/8に対して、x,yの交換を行なって求める。交換するとx=2y-5/8、したがって、y=(1/2)x + 5/16である。
一般にy=xに線対称な2本の直線は、片方がy=ax+bという形なら、残りはy=(1/a)x - b/aという形になる。つまり、傾き同士の積が1となる。これは、直交する2本の直線の傾き同士の積が-1になる、というよく使われる関係式によく似ている。きっと、またどこかの問題で使えるはずである。
確認のため、3次関数をもう一度書くと、
となる。
今回は、対称性の考察からx0 = -1/2という解を幸運にも見つけ出すことができた。因数分解により、残りの2つの解は2次方程式を解いて得ることができる。実数解の条件である判別式が正の場合(D=(4k+3)(4k-1) > 0)、 つまり k < -3/4、あるいはk > 1/4において、残る2つのの接点のx座標は
と計算される。
a=2x0、b=x02+k = 2(k + 1/4)x0 + k - 1/4を使って共通接線を引いてみると、「たすきがけの解」の意味あいがはっきりする。例によってpostscript言語によって図を描画してみると次のようになる。まずはわかりやすいk=1( > 1/4)の場合から。
 |
| k=1の場合。共通接線は3本引ける。赤線が「蛾の羽の先端解」。緑と青の線が「たすきがけの解」 |
次はいよいよk=-2 (< -3/4)の場合だ。「蛾の羽の先端解」以外の解が、果たして「たすき掛けの解」に似たようなものになっているのか、それとも全く異なる想像を絶するようなものなのか?
 |
| k=-2の場合。「たすき掛け」は放物線の「外」に出ている。 |
k < -3/4の領域でどのように3本の共通接線が存在できるのか、直感的な理解はできた。しかし、第二臨界点であるk= -3/4では、たった1本だった共通接線が、k < -3/4の領域に入った途端、突然3本に増加するという、このメカニズムは、いまだに理解しがたいものがある。なんとなく、蛾の羽の先端が開くとき、一気に縮退が解ける感じは想像できるのだが、図をつかってその様子を明らかにしておこう。
臨界点からわずかにずれた、k= -3.001/4.0 あたりを見てみよう。
 |
| k= - 3.001 / 4.0 の場合。 |
第一臨界点(k= 1/4)での縮退の正体は、共通接線が対称線y=xに重なるというものだった。たしかにy=xはy=xに対して「線対称」ではあるが、y=xとは直交してない。このため、縮退が解けても、線対称の関係にある青線と緑線の2本しか発生しなかったのである。直交する共通接線、つまり蛾の羽の先端解はひとり別のところ(x0=-1/2)で、y=xに直交する共通接線を作っていたのである。
さて、この辺りで試験問題の解答も解いておこう。a=2の場合である。問(1)ではb, kをaで表現したので、それを使えばよい。が、あの表式はa≠ -1, 0という縛りがあったのを忘れるべからず。とりあえず、a=2の計算はできるので計算すると、k = 3/8を得る。また、b = -5/8である。
今まで見た来たように、この問題でもっとも重要なのはパラメーターkである。k=3/8というのは第一臨界点k=1/4の上部、すなわち 3/8 > 1/4にある。この領域で、共通接線の数は3本あることを我々はすでに知っている。また、この時「蛾の羽の先端解」と「a=2に線対称な解」があることも我々はすでに知っている。蛾の羽の先端解の場合、傾きは常にa=-1である。接点はもう何度も出て来たようにx0=-1/2である。ここで導いた関係式b = -x02+kを使ってb=1/8が得られる。対称解は、すでに得られた答えy=2x-5/8に対して、x,yの交換を行なって求める。交換するとx=2y-5/8、したがって、y=(1/2)x + 5/16である。
一般にy=xに線対称な2本の直線は、片方がy=ax+bという形なら、残りはy=(1/a)x - b/aという形になる。つまり、傾き同士の積が1となる。これは、直交する2本の直線の傾き同士の積が-1になる、というよく使われる関係式によく似ている。きっと、またどこかの問題で使えるはずである。
2017年3月7日火曜日
東大2次試験(2017): 問題5(その2)
問(2) 傾きが2の共通接線が存在するようにkの値を定める。このとき、共通接線が3本存在することを示し、それらの傾きとy切片を求めよ。
この問題を解くには色々な方法があるだろうが、ここでは、前回求めた、放物線Cの接線の方程式
と、放物線D:y=x2+kの交点を求める方向性で解いてみる。接線と放物線の方程式を連立し、整理すると、2次方程式4x02x2+{4x0(k-x02)-1}x+(k-x02)2+k=0を得る。接線となるには判別式が0とならねばならないので、対応する条件式はx0に関しての3次方程式となる。
3次方程式の解の数は(複素解も含めれば)3つあるので、この条件式の意味するところは、共通接線の数は最大で3つまでということだ。kの値によって、この3次方程式の形は変わり、解の数は時には2つだったり、1つだったりするだろう。
物理では、こういう関数系の形状の変化を相転移と結びつけて考えることがよくある。また、φ4モデルという(素粒子物理における)場の理論では、「自発的対称性の破れ」の発生のメカニズムを、パラメータ(質量パラメータと呼ばれる)の変化によって議論する。これは、ノーベル賞を取った南部先生が提唱した考え方だし、同じくノーベル賞を受賞したヒッグスの提唱したヒッグス機構という理論でも似たような考え方を適用する。これらの理論はいわば「4次関数」の形状変化を質量パラメータによって追っていく形だが、ここでは3次関数の解の数をkというパラメータ(これは放物線の座標軸上の位置に相当)によって追っていく問題となっていて、なんとなく似ている。
3次方程式の解の公式はあるらしいのだが、高校でも、大学の物理学科でも、それは習わない。ただ、3次関数の微分は2次方程式になるので、極値が最大2つあることは明らかである。極値の正負をみると、3次関数が何回x軸を横切るか図形的に判断でき、そこから3次方程式の解の個数などの性質を議論することができる。
例えば、3次項の係数が正の場合、x→±∞に対し、3次関数は±∞にそれぞれ発散する。グラフ構造の詳細を気にしなければ(つまり大域的構造だけに着目すれば)、3次関数のグラフは「左から右にかけて(つまりxが負の領域から正の領域にかけて)」斜め右上に増加する関数とみなせる。ということは、必ずどこかでx軸をよぎることは保障される。そこで今度は詳細な構造に着目し、極大値が負値をとる場合を考える。このとき、極大点の左側において関数のグラフはx軸を横切れないから、解は一つしかないことが(図形的に)わかる。このような分析を、その他の場合についても行なえばよい。
「では早速微分してみよう」と行きたいところだが、 その前にこの三次関数についてもう少し分析しておく。これは、この問題に限ったことなので、他の問題で使えるとは限らない。が、少なくとも「対称性」の強みについて習熟する練習にはなる。
まず、前回、前々回に、図を描いて共通接線の本数の予想をした。特に注目するのは「蛾の羽の先端」型の共通接線だ。こういうタイプの接線は、放物線C、Dがxとyの交換に対して対称である、つまり直線y=xに対して線対称であることから、y=-x+bタイプに限られるのではないか?という予想がたつ。つまり線対称の直線y=xと直交する直線である。ちょっとでも直交からずれるようなことがあれば、接点にならないのではないか?というのが、対称性から引き出される直感である。実際、問題文でもa=-1の場合は特別視しているし、問(1)では行列式が0となってしまう値である。
問(1)の結果を用いると接点は x0=a/2で与えられる。a=-1を代入するとx0=-1/2となる。つまり、上の考察が正しいならば、x0の三次方程式の解の一つは常にx0=-1/2になるはずである。これは因数定理/剰余定理で確認するに値する。代入してみると
8(-1/2)3-16k(-1/2)2-8k(-1/2)+1=-1-4k+4k+1 = 0
となるではないか!つまり、予想通りa=-1は常に共通接線になっているのである。ここまでくれば、整式の割り算により因数分解をさらに進めることができ、
となる。したがって、共通接線の交点は、上の式の2次式の実数解の数で決まり、それは判別式で判定可能である。判別式は
D=(4k+1)2-4 =(4k+3)(4k-1)
と計算される。「臨界値」k=1/4が現れているのがわかる。このときD=0となるので、重解(共通接線はy=x)となる。3次方程式の解としてはx=-1/2(「蛾の羽の先端」解)と合わせて2つということになる。これは前々回の3つ目のグラフに相当する。
もう一つの「臨界値」らしきものとしてk=-3/4が見えてみる。このときD=0となって「重解」となるらしい。前々回の考察で、接線の数はk=1/4を臨界点として1つの場合と3つの場合(臨界点で2つ)に別れることはグラフを描いて推測した。このときk=-3/4というのはなかったはずだ。前回の考察を踏まえると、この第二「臨界点」は共通接線が1本の領域に属する。果たしてどんな「臨界値」なんだろうか?ここは考えても仕方ないので、グラフを描いてしまおう(試験会場でも手書きでやってみる価値はある)。
 |
| k=-3/4の場合 |
D>0, すなわち(4k+3)(4k-1)>0のとき、2つの異なる実数解が存在する。これはk<-3/4あるいはk>1/4の場合で、このとき共通接線は3本存在することになる。一方、D<0、すなわち(4k+3)(4k-1)<0のとき、実数解は存在しない。つまり、共通接線が1本しかないのは-3/4<k<1/4のときである。
まとめると、
k>1/4のとき、共通接線は3本。
k=1/4のとき、共通接線は2本。
-3/4<k<1/4のとき、共通接線は1本。
k=-3/4のとき、共通接線は1本。
k<-3/4のとき、共通接線は3本。
こうしてみると、(その0)のグラフによる分析で見たように、k=1/4は「連続的」な変化に見えるのに対し、k=-3/4は突如1本から3本に共通接線が増えるようにみえ、こちらは「相転移」に近い感じだ。果たして、k=-3/4における「相転移」とはどんなものなのだろうか?
2017年3月6日月曜日
東大2次試験(2017): 問題5(その1)
問1 直線y=ax+bが共通接線であるとき、aを用いてkとbを表せ。ただしa≠-1とする。
高校数学の立場からすれば、判別式を使うのが常套手段だろうが、ここでは微分計算や行列計算を取り込んだ手法を採用して、大学の物理で使う手法にできるだけ近づけてみよう。
まずは、陰関数(x=y2+k)が登場しているので、大学の力学や熱力学でよくつかう微分記号によって微分係数を求めることにする。
C: dy = 2xdx, D: dx = 2ydy
つまり、微分係数は
C: dy/dx = 2x
D: dy/dx = 1/(2y)
となる。
次に放物線Cにおける接点を(x0,y0)と置く。
このとき、共通接線の方程式は y-y0= 2x0(x-x0) と書ける。ただ、x0は放物線C上の点だからy0= x02+kという関係がある。これを使ってy0を消去すると
となる。したがって、y=ax+bが接線の表現だというならば、
Dの接線に関しても同じように計算を進めればよい。が、xとyの交換に関する対称性を利用すると少しだけ「退屈しのぎ」ができる。Dの接点を(x1,y1)とし、上の関係式でxとyを入れ替えた式x=2y1y-y12+kを考えるのである。この式とy=ax+bを比較して, y1を消去すれば, 4ab+4a2k=1という関係を得ることができる。
2つの式を(あえて)行列で表現すると
となる。左辺の行列の行列式は-16a(a+1)なので, a≠0, a≠-1の場合は逆行列が存在して
を計算すればbとkをaを使って表すことができる。計算結果は
となる。ただし、a≠-1, a≠0という条件があることを忘れぬようにしてないと、後でひっかかる。この場合には逆行列をとる前の関係式まで戻る必要がある。
a=-1のときは、Cから求めた条件式とDから求めた条件式が一致して、-4b+4k=1となるが、これ以上先に進むことはできない。またa=0の場合, 接線の形がy=bに限定されてしまう。Cに関してはb=kとすれば良いが、Dに関しては接線は引けなくなる。つまり、この場合は解なし、つまり共通接線はないということになる。
行列や行列式は量子力学や(解析)力学で出てくるので、大学に入る前に2x2行列くらいの計算は習熟しておきたいものだ。(でないと、教えるこちらが大変困る。)
高校数学の立場からすれば、判別式を使うのが常套手段だろうが、ここでは微分計算や行列計算を取り込んだ手法を採用して、大学の物理で使う手法にできるだけ近づけてみよう。
まずは、陰関数(x=y2+k)が登場しているので、大学の力学や熱力学でよくつかう微分記号によって微分係数を求めることにする。
C: dy = 2xdx, D: dx = 2ydy
つまり、微分係数は
C: dy/dx = 2x
D: dy/dx = 1/(2y)
となる。
次に放物線Cにおける接点を(x0,y0)と置く。
このとき、共通接線の方程式は y-y0= 2x0(x-x0) と書ける。ただ、x0は放物線C上の点だからy0= x02+kという関係がある。これを使ってy0を消去すると
となる。したがって、y=ax+bが接線の表現だというならば、
a = 2x0, b = -x02 + kという関係が成立する。この2式からx0を消去して整理すると-4b+4k=a2となる。
Dの接線に関しても同じように計算を進めればよい。が、xとyの交換に関する対称性を利用すると少しだけ「退屈しのぎ」ができる。Dの接点を(x1,y1)とし、上の関係式でxとyを入れ替えた式x=2y1y-y12+kを考えるのである。この式とy=ax+bを比較して, y1を消去すれば, 4ab+4a2k=1という関係を得ることができる。
2つの式を(あえて)行列で表現すると
となる。左辺の行列の行列式は-16a(a+1)なので, a≠0, a≠-1の場合は逆行列が存在して
を計算すればbとkをaを使って表すことができる。計算結果は
となる。ただし、a≠-1, a≠0という条件があることを忘れぬようにしてないと、後でひっかかる。この場合には逆行列をとる前の関係式まで戻る必要がある。
a=-1のときは、Cから求めた条件式とDから求めた条件式が一致して、-4b+4k=1となるが、これ以上先に進むことはできない。またa=0の場合, 接線の形がy=bに限定されてしまう。Cに関してはb=kとすれば良いが、Dに関しては接線は引けなくなる。つまり、この場合は解なし、つまり共通接線はないということになる。
 |
| a=-1の場合 (クリックして拡大) |
2017年3月5日日曜日
東大2次試験(2017): 問題5(その0)
引き続き、2017年の問題を見てみる。今度は問題5。
問題4でもちょっと議論したが、この問題でも「対称性」の考え方が利用できる。というより、こちらの問題の方がもっと明示的な形で対称性が見えるので、問題を解く前に、まずは直接グラフ化して、この問題と物理学との関連性を見てみよう。
[対称性について]
この問題の対称性はxとyの交換に対する対称性である。 放物線CとDはこの交換によって、入れ替わる。つまり、CとDのグラフはy=xに対して線対称の関係があることがわかる。まずはk=4の場合について図示してみよう。
試験問題では、CとDの共通接線を考えることになるのだが、その観点からすると、グラフのタイプ はパラメータkによって分類できることが推測される。上の場合は放物線がy=xと交わらないタイプ。
次は、交わってしまうタイプを見てみよう。k=-3に選んである。
なんとなく、蛾のような蝶のような形に見えるが、共通接線は「羽」の先端に一本しか引けないような気がする。k=4の場合は、なんとなくタスキがけに行けそうな気もしないでもないが、確信は持てない。ただ、問(2)で3本の共通接線...とかなんとか言っているので、この場合なのかもしれない。
こうなってくると、y=xと交じる、交じらない、の中間の場合、つまり接する場合が気になってくる。こういうのは、物理では「臨界点」とかいうときもあるのだが、この問題ではk=1/4の場合がそれにあたる。
この場合の共通接線の一つはy=xであるから、共通接線は2本引けることが予想される。そうすると、k>1/4の場合はやっぱりタスキがけの2本と、「羽の先端」に一本と、全部で3本ありそうな気もしてくる。
超流動の研究で、臨界温度Tcというのが出てくるが、臨界値を境に、超流動状態と常流動状態が相転移する。この問題でもk=1/4が臨界値になって、共通接線の本数が変化すると考えれば面白いだろう。共通接線の数は自然数だから、この「転移」は「連続変化」である。が、一応「量子化」されているので「相転移」と呼んでもいいのかも...
この「臨界値」の求めるには、当然ながらy=xとy=x2+k(あるいはx=y2+k)の連立方程式(2次方程式)の、判別式=0を解けばよい。臨界値k=1/4の「4」は、判別式の公式、D=b2-4acの4に由来する(この2次方程式の係数はa=1, b=-1, c=kなので)。
 | ||
| 問題文はクリックすると拡大できる。 |
[対称性について]
この問題の対称性はxとyの交換に対する対称性である。 放物線CとDはこの交換によって、入れ替わる。つまり、CとDのグラフはy=xに対して線対称の関係があることがわかる。まずはk=4の場合について図示してみよう。
 |
| k=4の場合。y=xに対してCとDは対称になっている。 |
試験問題では、CとDの共通接線を考えることになるのだが、その観点からすると、グラフのタイプ はパラメータkによって分類できることが推測される。上の場合は放物線がy=xと交わらないタイプ。
次は、交わってしまうタイプを見てみよう。k=-3に選んである。
 |
| k=-3の場合。 |
こうなってくると、y=xと交じる、交じらない、の中間の場合、つまり接する場合が気になってくる。こういうのは、物理では「臨界点」とかいうときもあるのだが、この問題ではk=1/4の場合がそれにあたる。
 |
| k=1/4の場合。 |
超流動の研究で、臨界温度Tcというのが出てくるが、臨界値を境に、超流動状態と常流動状態が相転移する。この問題でもk=1/4が臨界値になって、共通接線の本数が変化すると考えれば面白いだろう。共通接線の数は自然数だから、この「転移」は「連続変化」である。が、一応「量子化」されているので「相転移」と呼んでもいいのかも...
この「臨界値」の求めるには、当然ながらy=xとy=x2+k(あるいはx=y2+k)の連立方程式(2次方程式)の、判別式=0を解けばよい。臨界値k=1/4の「4」は、判別式の公式、D=b2-4acの4に由来する(この2次方程式の係数はa=1, b=-1, c=kなので)。
2017年3月4日土曜日
東大2次試験(2017): 問題4(その4)
問(3)まではものの5分から10分ほどで到達できたのだが、問(4)には苦戦した。最大公約数というのは物理ではあまり使わない...というのは言い訳になるので、この辺でやめておこう。
まず、問(3)の結果から、全てのnにおいて、数列の要素anは約数2を持つことがすぐに結論できる。それはkが偶数の場合の因数1+(-1)k=2に由来する。この「2」はkにもnにも依存しない共通の因数であるから、任意のnに対して、an+1とanの最大公約数の第一候補に挙げられる。実際、n=1,2,3,4あたりまで具体例で計算してみると2が正解らしいことが推測されるし、実際の正解も2である。
気になるのは、特別なnの値、例えばn=n1において、偶然n1に依存するような形で公約数が現れはしないか?という疑問である。もしn1が非常に大きな数、たとえばn1=123456789とかだったとしたら、n=1,2,3,4あたりまで具体例で計算したら2でした、なんてのは無駄な話となる。
n=n1でan1 とan1+1が公約数Lを偶然持ったとする。すると、(2)で得た漸化式a1an = an+1 - an-1 によって、an1+2も公約数Lを持つことになる。つまり、偶然どこかで公約数が偶然変更されるようなことがあれば、それはその後の要素にも引き継がれることになる。つまりn>n1に属する任意のnにおいて、an+1とanの間に、nに依存しない最大公約数2Lが存在することになる。果たして、こんなことがあるかどうか調べてみよう。
まずは2項展開で得た式を見直してみる。ただし、和の部分はkについて偶数だけをとる、とせずにk=2jと書いてj=0, 1, 2,...で和をとるように書き直す。すると
となる。和に関するjの上限値はガウス記号と呼ばれる[n/2]で与えられる。これはn/2を越えない最大の整数という意味を持つが、若干鬱陶しいので、n=2m+1(奇数)のときと、n=2m(偶数)のときとで場合分けする。双方の場合について[n/2]=mとなる。
和の部分を具体的に書き下してみる。まずは奇数の場合(n=2m+1)から。ガウス記号が効いて、二項展開の最後の項は省かれてしまうため、
となる。各項をよくみると、μが共通因子となって取り出せることがわかる。したがって、nが奇数の場合は
と因数分解できる。ただしn=2m+1として、
である。初項(最終項)は、μ(ν)のみの2m(m)次式がになっているので、互いに素の場合には(自明な)共通因子は存在しない。
次に、nが偶数の場合は和の部分は二項展開における最高次の項がμに関してもνに関しても取り込まれるので、μとνが互いに素の場合には、新たな(自明な)共通因子はない。したがって、
ただし、n=2mとして
である。
問題ではμ=2, ν=5であり、共に素数である。この場合はNmもMmもともに奇数であることは容易にわかる。(それぞれの最終項は奇数だが、それ以外項はは2の倍数になっているので。)また、2と5は当然互いに素なので、μとνの間に公約数はない。
NmもMmも奇数であるから、もしこれが因数分解できるとしたら、それは奇数同士の積となる。したがって、Nmがたまたま偶数となって、nが奇数の場合の因数2μ=4が公約数になることはない。つまり4が最大公倍数になることはない。最大公倍数は2あるいは2×奇数の形になる。
上で考察したように、 仮にあるn=n1において、たまたま奇数の因数2L+1がNmとMmに発生したとする。しかし、この因数はn>n1でも因数となり続けることも上で確認した。だとすると、NmやMmの中に、mに依存しない共通因数がn>n1において延々と発生し続けることになるが、MmやNmはμとνの多項式であり(μとνは互いに素)、どの項もmに依存した数になっているので、この多項式がmに依存しない因数を含むことはありえない。
問 (4) an+1 と an の最大公約数を求めよ。nが偶数でも奇数でも、隣り合う、「パリティ」の異なる2種類の数列要素の間の最大公約数を考えることになるので、考え方は同じになる。従って、nを偶数と仮定して議論を進める。(nが奇数の場合は、議論の中で「パリティ」の異なる成分に入れ替えるだけでよい。)
まず、問(3)の結果から、全てのnにおいて、数列の要素anは約数2を持つことがすぐに結論できる。それはkが偶数の場合の因数1+(-1)k=2に由来する。この「2」はkにもnにも依存しない共通の因数であるから、任意のnに対して、an+1とanの最大公約数の第一候補に挙げられる。実際、n=1,2,3,4あたりまで具体例で計算してみると2が正解らしいことが推測されるし、実際の正解も2である。
気になるのは、特別なnの値、例えばn=n1において、偶然n1に依存するような形で公約数が現れはしないか?という疑問である。もしn1が非常に大きな数、たとえばn1=123456789とかだったとしたら、n=1,2,3,4あたりまで具体例で計算したら2でした、なんてのは無駄な話となる。
n=n1でan1 とan1+1が公約数Lを偶然持ったとする。すると、(2)で得た漸化式a1an = an+1 - an-1 によって、an1+2も公約数Lを持つことになる。つまり、偶然どこかで公約数が偶然変更されるようなことがあれば、それはその後の要素にも引き継がれることになる。つまりn>n1に属する任意のnにおいて、an+1とanの間に、nに依存しない最大公約数2Lが存在することになる。果たして、こんなことがあるかどうか調べてみよう。
まずは2項展開で得た式を見直してみる。ただし、和の部分はkについて偶数だけをとる、とせずにk=2jと書いてj=0, 1, 2,...で和をとるように書き直す。すると
和の部分を具体的に書き下してみる。まずは奇数の場合(n=2m+1)から。ガウス記号が効いて、二項展開の最後の項は省かれてしまうため、
となる。各項をよくみると、μが共通因子となって取り出せることがわかる。したがって、nが奇数の場合は
と因数分解できる。ただしn=2m+1として、
である。初項(最終項)は、μ(ν)のみの2m(m)次式がになっているので、互いに素の場合には(自明な)共通因子は存在しない。
次に、nが偶数の場合は和の部分は二項展開における最高次の項がμに関してもνに関しても取り込まれるので、μとνが互いに素の場合には、新たな(自明な)共通因子はない。したがって、
ただし、n=2mとして
である。
問題ではμ=2, ν=5であり、共に素数である。この場合はNmもMmもともに奇数であることは容易にわかる。(それぞれの最終項は奇数だが、それ以外項はは2の倍数になっているので。)また、2と5は当然互いに素なので、μとνの間に公約数はない。
NmもMmも奇数であるから、もしこれが因数分解できるとしたら、それは奇数同士の積となる。したがって、Nmがたまたま偶数となって、nが奇数の場合の因数2μ=4が公約数になることはない。つまり4が最大公倍数になることはない。最大公倍数は2あるいは2×奇数の形になる。
上で考察したように、 仮にあるn=n1において、たまたま奇数の因数2L+1がNmとMmに発生したとする。しかし、この因数はn>n1でも因数となり続けることも上で確認した。だとすると、NmやMmの中に、mに依存しない共通因数がn>n1において延々と発生し続けることになるが、MmやNmはμとνの多項式であり(μとνは互いに素)、どの項もmに依存した数になっているので、この多項式がmに依存しない因数を含むことはありえない。
2017年3月3日金曜日
東大2次試験(2017): 問題4(その3)
問(2)で、μと√νの部分に分ける考え方を少しやった。また、逆数1/p=qを考えることで、μの符号を反転できることもみた。この考え方を推し進めて、問(3)を解いてみる。
ここでは二項展開の公式を利用して、物理でよく使う「パリティ」によく似た考え方で問題を分析してみよう。まずは公式をそのまま展開して、p2がμと√νの(有限項の)積和で書けることを確認する。
nCkもμのベキ乗も自然数である。その積も和も自然数の集合からはみ出すことはない。しかし、√νのベキ乗はkが偶数のときは自然数だが、奇数の場合は無理数となってしまう。無理数と自然数の和、あるいは積は無理数となるから、pnは一般には無理数である。
ただ、この問題で登場する無理数は平方根√νだけであり、その奇数べきはνm√νという形に限られるから、pnは自然数の部分と、自然数×√νという部分との和の形になる。pの逆数q=1/pはμの符号反転させるので、うまい具合に√νに比例する部分が相殺してくれたら、anは自然数になるだろう、という予想が立つ。
実際、逆数のべきを二項展開すると
となるので、和か差をとればうまく消えてくれそうである。
anを計算してみると
となる。ただし(-1)2n=1を利用した。kが奇数の項は最後の因子が0となるので消えてしまうので、kが偶数の項の和だけをとることになる。またこのとき(√ν)kはうまい具合に平方根が消えて自然数になってくれる。したがって、自然数同士の積の和によってanは表現されていることになるので、anは自然数からはみ出さないことがわかる。
ちなみに、物理学では、σk=1+(-)kというタイプの因子は、量子力学における波動関数のパリティや、対称/反対称性の議論で よく出てくる。実際、大学3年ごろになると、1次元井戸型ポテンシャルの量子化について習うことになるだろうが、kを量子数とみなし、波動関数の分類に役立つことを学ぶことだろう。
量子力学の波動関数の対称性の議論では、力学変数qの符号を変えたときの波動関数ψ(q)の対称性を考える。そのときψ(-q)=ψ(q)なら対称、ψ(-q)=-ψ(q)なら反対称と呼んで区別する。一次元の問題では、両者は直交し、一次独立な解になる。
この問題ではp→1/p (つまりpとqを交換する変換に相当)とする操作に対し、
an = pn+(-q)n→(-)n(pn+(-q)n)=(-)nanという対称性がある。σ=(-)nがパリティ(あるいはシグナチャーと呼んでもよいかも)のような量に相当するという訳だ。nが奇数とき「反対称」、nが偶数のとき「対称」と呼んで良いだろう。
σの値は+1あるいは−1だが、どちらの値の場合でも、anは(自然数という)同じ種類の集合に属するということを示したのがこの問題といえる(どちらかは無理数になり、どちらかは自然数になる、とかいうことはないという意味)。こういう証明は物理ではときどき必要になる。たとえば、SO(3)に属する力学変数ならその行列表現Aは必ずdet (A)=1を満たさなければならない..などなど。
(3)anが自然数であることを示せ。この問題で登場する自然数はμ=2とν=5である。これらの和/差そして積の組み合わせで表現されるのがanである。a1もa2も自然数であることは問(1)で確認したので、n>2においてもanが自然数という集合から抜け出していかない(はみ出していかない)ことを示すのがこの問題である。(ちなみに自然数の集合は、割り算に対して「はみ出してしまう」性質がある。例えば2÷3は自然数ではなく、より広い有理数へとはみ出す。)
ここでは二項展開の公式を利用して、物理でよく使う「パリティ」によく似た考え方で問題を分析してみよう。まずは公式をそのまま展開して、p2がμと√νの(有限項の)積和で書けることを確認する。
nCkもμのベキ乗も自然数である。その積も和も自然数の集合からはみ出すことはない。しかし、√νのベキ乗はkが偶数のときは自然数だが、奇数の場合は無理数となってしまう。無理数と自然数の和、あるいは積は無理数となるから、pnは一般には無理数である。
ただ、この問題で登場する無理数は平方根√νだけであり、その奇数べきはνm√νという形に限られるから、pnは自然数の部分と、自然数×√νという部分との和の形になる。pの逆数q=1/pはμの符号反転させるので、うまい具合に√νに比例する部分が相殺してくれたら、anは自然数になるだろう、という予想が立つ。
実際、逆数のべきを二項展開すると
となるので、和か差をとればうまく消えてくれそうである。
anを計算してみると
ちなみに、物理学では、σk=1+(-)kというタイプの因子は、量子力学における波動関数のパリティや、対称/反対称性の議論で よく出てくる。実際、大学3年ごろになると、1次元井戸型ポテンシャルの量子化について習うことになるだろうが、kを量子数とみなし、波動関数の分類に役立つことを学ぶことだろう。
量子力学の波動関数の対称性の議論では、力学変数qの符号を変えたときの波動関数ψ(q)の対称性を考える。そのときψ(-q)=ψ(q)なら対称、ψ(-q)=-ψ(q)なら反対称と呼んで区別する。一次元の問題では、両者は直交し、一次独立な解になる。
この問題ではp→1/p (つまりpとqを交換する変換に相当)とする操作に対し、
an = pn+(-q)n→(-)n(pn+(-q)n)=(-)nanという対称性がある。σ=(-)nがパリティ(あるいはシグナチャーと呼んでもよいかも)のような量に相当するという訳だ。nが奇数とき「反対称」、nが偶数のとき「対称」と呼んで良いだろう。
σの値は+1あるいは−1だが、どちらの値の場合でも、anは(自然数という)同じ種類の集合に属するということを示したのがこの問題といえる(どちらかは無理数になり、どちらかは自然数になる、とかいうことはないという意味)。こういう証明は物理ではときどき必要になる。たとえば、SO(3)に属する力学変数ならその行列表現Aは必ずdet (A)=1を満たさなければならない..などなど。
2017年3月2日木曜日
東大2次試験(2017): 問題4(その2)
(2) n ≧ 2とする。積a1an を, an+1 とan−1 を用いて表せ。
pn±1 =pn·p±1=pn(±2+√5)である。q=p-1=-2+√5に注意。また、
となる。ただし新しい数列bnを
と定義した。bnが消去できるのがここでのポイントである。それには「差」を考えればよく、
を得る。a1=4であることに気をつけると求める解答は a1an = an+1 - an-1となる。
東大2次試験(2017): 問題4(その1)
問(1)はa1とa2を計算するだけの、試験問題としては簡単なものだ。教育的には、無理数の四則演算に関しての習熟度を問う、とかいうのが目的なんだろう。
力学的、あるいは量子力学的に(無理に考えれば)、2回の微分方程式を級数展開法で解く際に必要となる、2つの初期条件、あるいは級数の係数数列の最初の2つの要素の値、に相当するといえるのかも。
もっと簡単に考えれば、例えばある時間tにおける質点の位置x(t)を計算するときは、それより前の時間、例えばt-Δtにおいて測定した少なくとも2つの物理量必要だということだ。つまりx(t) = x(t-Δt)+v(t-Δt)Δt+....となるが、これはテイラー展開の考え方でもある。0<Δt<<1が満たされれば、この式の精度はよくなる。
また、数学的に見れば、フィボナッチ数列のように、an+1をanとan-1から導出するという考え方に準拠したものと言えるかもしれない。フィボナッチ数列は漸化式an+1=an+an-1によって生成されるが、最初にa1とa2を与えておかなければことは始まらない。通常はa1=a2=1とする。
(1) p-qの計算では、前回も書いたように、p=2+√5とおいた時に
が成り立つことに、まずは気づいて欲しいという「親心」だろうと思う。p-qという量は差であり、整数を与える。これをa1とおくというわけだ。答えは、a1=2x2=4。
(2)次はp2+q2 の計算。前回、これも基本量であると考察した。pq=1という重要な関係に注意すると、(p+q)2=p2+q2+2である。これを利用してp2+q2=(2√5)2 - 2 = 18=a2が得られる。試験問題的にはp-qが(1)で計算してあるのだから、(p-q)2=p2+q2-2とするのが普通だろう。
力学的、あるいは量子力学的に(無理に考えれば)、2回の微分方程式を級数展開法で解く際に必要となる、2つの初期条件、あるいは級数の係数数列の最初の2つの要素の値、に相当するといえるのかも。
もっと簡単に考えれば、例えばある時間tにおける質点の位置x(t)を計算するときは、それより前の時間、例えばt-Δtにおいて測定した少なくとも2つの物理量必要だということだ。つまりx(t) = x(t-Δt)+v(t-Δt)Δt+....となるが、これはテイラー展開の考え方でもある。0<Δt<<1が満たされれば、この式の精度はよくなる。
また、数学的に見れば、フィボナッチ数列のように、an+1をanとan-1から導出するという考え方に準拠したものと言えるかもしれない。フィボナッチ数列は漸化式an+1=an+an-1によって生成されるが、最初にa1とa2を与えておかなければことは始まらない。通常はa1=a2=1とする。
(1) p-qの計算では、前回も書いたように、p=2+√5とおいた時に
が成り立つことに、まずは気づいて欲しいという「親心」だろうと思う。p-qという量は差であり、整数を与える。これをa1とおくというわけだ。答えは、a1=2x2=4。
(2)次はp2+q2 の計算。前回、これも基本量であると考察した。pq=1という重要な関係に注意すると、(p+q)2=p2+q2+2である。これを利用してp2+q2=(2√5)2 - 2 = 18=a2が得られる。試験問題的にはp-qが(1)で計算してあるのだから、(p-q)2=p2+q2-2とするのが普通だろう。
2017年3月1日水曜日
東大2次試験(2017): 問題4(その0)
行列の問題が高校数学から削除されてしまい、しばらくやる気が無くなってしまった。
そもそも、研究で使う量子力学なら、面白い切り口で高校数学と向き合えるかな、と思ったのがこのブログを書き始めた主な動機だったから、行列がなくなったのは痛手だった。
最近、力学など大学初年度の物理を担当するようになって、自分の知識に幅が出て来たのと、研究でも数理物理的なテーマに興味を持ち始めたので、行列でなくても何か議論できるかもと思い直した。特に、整数の問題は面白いものが多いので、手始めに今年の東大の2次試験の四番から再開してみようと思う。
前置きはこのくらいにしておいて、さっそく問題の分析に入ろう。この問題は整式とか、多項式とか、素数とかが中心にあるのだが、面白いことに無理数p=2+√5が初っ端に登場する。ポイントはpの逆数がpと密接に関連するような特別な無理数を選んでいるところだ。この性質により、様々な面白いことが発生する。
まず2つの自然数μ, νを使って無理数pを,
と表すことにする。この問題ではμとνの間に特別な関係を設定して、逆数1/p=qが
となるようにしている点が面白い。これが成り立つためのμとνの関係式は
である。試験問題で採用された具体的な値はμ=2, ν=5である。
数式になんらかの対称性(あるいは特別な性質)を要求し、それが成立するための条件式を見出すというのは、量子力学の手法に似ていなくもない。一旦このタイプの「対称性」に気がつけば、おもしろい問題をいろいろとアレンジすることが可能だ。
pとqがこのような関係にあれば, p+qは「純」無理数(ここでは、平方根だけで表現されるという意味)の2√νとなるし、p-qは自然数2μになる。この問題を整数問題にしたければ、p-qと(p+q)2を使うことになる。ただし、後者の量に関しては、pq=1なので、(p+q)2=p2+q2+2となる。したがって、実質的にはp-qとp2+q2が基本量ということになるだろう。(p-q)2=p2+q2-2だから、これは実質的にはp2+q2に等価な量だ。
「これ以外の新しい量を探す」という観点からすると、次は(p-q)3ということになるだろう。これも展開すると
となるので、新たな基本量としてはp3-q3ということになるだろう。このようにして問題で与えられた数列anが規定されたと考えられる。
登録:
投稿 (Atom)