東大２次試験（２０１３）：問題４

図形の問題だが、ベクトルが問題文に与えられているから、ベクトルで解こう。前にも述べたようにベクトルと行列は密接な関係にある。量子力学では両者は切っても切れない関係にある。だから、この問題もその練習だと思って解いていこう。さもないと、古代ギリシャの幾何学の学校で勉強させられてる気分になってしまう...

とはいえ、まずは古代ギリシア風に解いてみよう。ちなみに（１）はとても簡単で、センター試験でやるような問題といってもいいだろう。なんの工夫も要らない、そのまま正直にやるだけで答えが出てくる。問われているのは角度。角度をベクトルで表現するとしたら、まずは「内積」が思い浮かぶ。

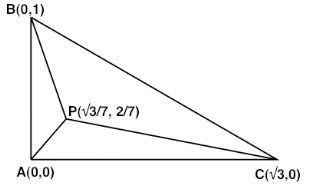得られた答えを基に、postscriptで作図してみた。

まずは、PAとPBのなす角をφ、PAとPCのなす角をθとおこう。PCとPBのなす角は自動的に2π-φ-θとなるが、何度も書くのが面倒なので、これをχとおくことにする。したがって、φ+θ+χ=2π。PAとPBの内積を(PA・PB)と表すことにすると、(PA・PB)=|PA| |PB| cosφだ。同様にして、(PA・PC)などの内積もベクトルの長さと角度によって表される。与えられた式に対し、最初はPAで内積をとり、次はPBで、最後はPCという具合に３種類の内積をとる。例えば、PAの場合は(PA・PA)/|PA| +(PA・PB)/|PB| +(PA・PC)/|PC| = 0となる。これに角度や長さ（ノルム）の表現を代入すると、1 + cosφ + cosθ = 0という関係式が手に入る。このようにして、角度に関しての方程式が３つ手に入り、その連立方程式を解くと、cosφ=cosθ=cosχ=-1/2となる。つまり、φ=θ=χ=2π/3という答えが得られる。

実は、与えられた与式、３つの単位ベクトルの和が０ベクトル、は物理的に考えれば、３つの力の釣り合いを表している。全てが同じ大きさ（単位ベクトル）なので、１２０度を成して引っ張り合ったときだけ釣り合うことは直感的にすぐわかる。もちろん、これは東大の数学の試験なので、答えはわかっても「数学の答案らしく」仕上げないといけないので、上のような計算をやってみせればよい。いずれにせよ、あっという間にここまでは来れる。

次の（２）がちょっと厄介だ。（２）もセンター試験風に簡単に解けるのであれば、これはもはやセンター試験であって、東大の二次試験ではない。つまり、そうは問屋が下ろさない、というわけだ。（１）が解けた段階で、すぐに点A、B、C、Pを結んで出来る複数の三角形について、誰もが余弦定理を使いたくなるはずだ。しかし、余弦定理で行き着けるのは、(a-b)(a+b+c)=-1などの関係式３つに過ぎず、なかなかその先に進む事ができない。a+b+c=kなどとおいて技巧的に、かつかなり強引に解き進む方法もあるらしいが、ここでは行列とベクトルの方法で解く事にしよう。古代ギリシアの幾何学ではなく、あくまで、デカルトが創始した、近代ヨーロッパの「代数幾何」として解くのだ！

まず、２次元平面における直線のパラメータ表示を使う。これは前に、東大(1977)の問題を研究したときに利用した方法だ。（注意：現在このテーマは「その１」までで中断されているが、手元のメモにはちゃんと書いてあるので....そのうち更新しますから、少々お待ちください。）Aを原点とし、ABをy軸、ACをx軸とする座標をセットすると、ベクトルPB、PA、ABの関係は、AB=AP+PBとなる。ベクトルPAを極座標表示するとPA=(a cosθ,a sinθ)=a e(A)となる。ここで、e(A)=(cosθ,sinθ）はAP方向の単位ベクトルを表す。つまり、-PA/|PA|=e(A)。AB=(0,1)は自明。そして、PB=b R(π/3)e(A)と書ける。R(φ）は回転角φの回転行列。bR(π/3)は、今年の問題（１）で登場した行列Aと同じ構造をしている、つまりスケーリングと回転の組み合わせだ。

PとBを通る直線というのは、APを起点にPCの方向に伸びる直線のことだ。だから、e(B)=R(2π/3)e(A)を基本ベクトルとし、そのベクトルをPの先から延ばしたり縮めたりして直線PBを「作る」ことになる。伸び縮み（スケーリング）の程度がbということになる。e(B)は単位ベクトルe(A)を回転させただけだから、長さは１のまま。つまり、PB方向の単位ベクトルということになる。当然、e(A)とe(B)は一次独立となる。２次元平面上のどんなベクトルも２つの一次独立なベクトル（基底ベクトル）の線形結合で表す事ができる、というのが線形代数の大事なポイントだ（定理になっているはず）。この場合は、直線PB上にある点に向けて、原点Aから伸びるベクトル（y軸のこと）が、e(A)とe(B)の線形結合になっているというふうに解釈する。（もちろん、直線のパラメータ表示と見てもよい。）まとめると、

式(1)

となるが、よく考えると(cosθ,sinθ)=R(θ)(1,0)であり、R(A)R(B)=R(A+B)だから、

式(2)

と書く事もできる。この結果は、x軸方向の単位ベクトルを９０度反時計周りに回転して、y軸の単位ベクトルに変換した、と見なすことができる。つまり、

式(3)

という関係式が導ける。この関係式から得られるのは、aとbに関する連立一次方程式で、それを行列、ベクトルを用いてまとめると、

式(4)

となる。この行列は逆行列をもつ（行列式=√3/2となり、０でない）から、両辺にそれをかけて(a,b)を求めることができた。ただし、ここまでの計算ではaもbもθによるパラメータ表示になっているので、最終的にはθを消去する必要がある。この段階では、それがどのように実現されるのかはまだ明らかではない。が、計算を先に進めよう。

次は、同じようにして直線PCのパラメータ表示から出発して、(a,c)を計算することができる。重要なのは

式(5)

だ。これは、直線PCのパラメータ表示が、x軸にある単位ベクトルを、x軸に沿って√３倍に拡大する操作と等価、という結論を意味する。この式から、(a,c)を計算することが可能だ。

最初の連立方程式を解いて得られたaはa=-(2/√3)cos(θ+π/3)、次の連立方程式からはa=-2sin(θ-π/3)が得られた。一見異なる表式だが、同じ値を持たなくてはならない。したがって、両者を結ぶ必要がある。その結果θに関する方程式が得られ、tanθ=2/√3という値が求まる。これはcosθ=√3/√7、sinθ=2/√7を意味する。θの値が決まったので、a,b,cのパラメータ表示からθを消去すると、(a,b,c)=(1/√7, 2/√7, 4/√7)という答えが得られる。

考察：

結局(a,b,c,θ)という４つの変数に対して、４つの「一次連立方程式」を立てる事ができたのが勝因だ。とはいえ、素直な連立方程式ではなく、θに関してはaのダブりをうまく利用して求めることになった。ある意味、これは「運」だったのかもしれない。

とはいえ、直線のパラメータ表示を、回転や拡大の組み合わせとして理解できたのは面白かった。結局直線が三角形の頂点にやってくる、というのはかなり強い拘束条件であって、いろいろな値が決まるのだ。それにしても、この問題を考えついた人は、かなり図形とにらめっこしたと思われる。もちろん、強い拘束条件があるので、必ず答えが得られるはず、と信念をもって細部を確認していったと思う。３本の単位ベクトルの釣り合いではなく、比率を変えて同じような問題を作ってみたら、果たして答えは求まるのだろうか？興味が出て来た。