センター試験の数I(その５）

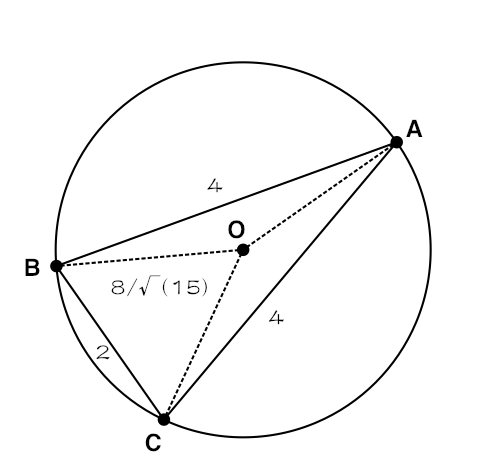
まずは図に、与えられた条件を書き込む。

AB=4, BC=2, cosθ=1/4が与えられた情報（θは角ABC)。

この情報を使って、まずはACを計算する。これは素直に余弦定理を適用すればよい。すなわち、AC²=4²+2²-2・4・2・cosθ = 16+4-4 = 16.つまりAC=4となって、三角形ABCは二等辺三角形ということがわかる。つまり角ABC=角ACB

また、sin²θ=1-(1/4)²=15/16、よってsinθ= √15/4はすぐに求まるが、これは外接円の半径を正弦定理で求めるための準備。正弦定理よりR=(1/2)(4/sinθ）= 8√15 / 15を得る。または、正弦定理を忘れてしまった人は、角AOC=2×角ABC=2θであることを利用し、三角形AOCに余弦定理を適用すればよい。すなわち、4²=2R²-2R²cos(2θ)=2R²(1-1+2sin²θ）=4R²(15/16)より答を得る。