逆行列の定義

二次形式の考察をしているとき、逆行列の定義が引っかかったので、勉強し直してみた。これが意外にも難しいことがわかった。今まで、逆行列の定義はすんなり受け入れてきたので、ちょっとショックだ。

まずは通常の定義を確認しよう。n次元の正方行列を２つ考え、それぞれをA, Xと書くことにする。単位行列をEとすると、AX=XA=Eが成り立つ時、XをAの逆行列という。（逆に、AはXの逆行列だと言ってもいい。）X=A^-1と表すことが多い。

高校までにおいては２次元の場合しか考察しないが、大学に入ると一般のn次元の場合について考える。その場合の逆行列を与える公式（Cramerの公式ともいう）によると、余因子行列の転置行列に、行列式の逆数をかけたものが、逆行列となる。（余因子については、ここでは説明するのは省略し、別の機会で与えることにする。）この公式から明らかにわかるのは、逆行列の存在は、行列式の逆数が存在するかどうかにかかっているということだ。つまり、行列式が０となる場合には、その逆行列は存在しないということだ。逆行列が存在する時、その行列は「正則である」という（英語ではnon-singularという）。

この条件（つまり逆行列が存在するための条件）は高校でも教わるが、二次元の場合に限られる。二次元の場合の行列式は簡単なので、逆行列が存在するかはすぐにチェックできる。例えば、二次元正方行列Aが

式（１）

で与えられるならば、その行列式det(A)は、

式（２）

となる。この式の幾何学的な解釈については以前議論した。det(A)=0ならAの逆行列は存在しないが、det(A)が０でなければ逆行列A^-1は存在し、

式（３）

となる。

さて、今回気になったのは、AX=Eが成立するのはいいとして、XA=Eが成立することも条件として組み込まなくてはいけないのかどうか？という点だ。逆行列の定義として、かならず「AX=XA=E」と書かれるけれど、AX=Eだけが成立していれば、XA=Eは導出できるのではないか？この問題を書き換えれば、「任意の正方行列Aに対し、AX=Eが成立するXが見つかった時、XA=Eが成立しないようなXは存在するかどうか？」という問題となる。

予想としては、「存在しないんじゃない？」といきたいところだが、果たしてそうなのかどうかは調べてみないといけない。

ちなみに、これに似たような感じの問題が、東大(2007)の第４問に出題されている。

（１）実数aに対し、2次の正方行列A, P, Qが、５つの条件A=aP+(a+1)Q、P² =P, Q²=Q, PQ=O, QP=Oを満たすとする。このとき、(P+Q)A=Aが成り立つことを示せ。

(2),(3)は関係ないので省略。また、この問題自身はとても簡単で、正直に左辺の(P+Q)Aを与えられた条件を利用しながら計算するだけだ。

今、気にしているのは逆行列の定義の方だが、この問題では逆行列の定義自身は直接問われてはいない。が似たような状況が問題で与えられている。それは(P+Q)A=Aなのだが、ここから自動的にP+Q=Eと言えるのかどうかが気になる。もしAに逆行列が存在するならば、自明な結論としてP+Q=Eを得る。しかし、Aに逆行列がないとするならばどうなのだろうか？逆行列が無い場合には、P+Q=EとはならないP+Qが存在して、それが(P+Q)A=Aを満たすというのだろうか？この問題ではAは二次正方行列なので、具体的に書き下して「実験」してみよう。逆行列をもたないAの例として、

式（４）

を考える。P+QをBとおいて、BA=Aを満たすBを求めてみる。すると、答えは一つにはきまらないが、例えば、

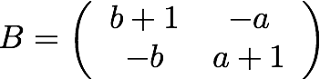式（５）

が条件を満たす。しかし、このBは単位行列とは限らない。(a=b=0の場合のみが単位行列、しかしそのときA=Oとなってしまう。）結論としては、BA=Aだからといって、B=Eかどうかは決定できないということになる。

さて、本題に戻ろう。今度はAB=Eのとき、B=A^-1と言えるかどうか？という問題だ。もしこれが言えれば、自動的にBA=Eは成立する。

両辺の行列式を取ってみると、det(A) det(B)=1となる。この結果、det(A)=0は許されない(同時にdet(B)=0も許されない）ことがわかる。従って、逆行列は存在することになり、BA=Eは自動的に成立する。この証明は一般のn次の場合にも適用できる。

しかし、問題になるのは、Cramerの公式を導くときに、逆行列の定義としてAB=BA=Eを利用したかどうかだ。もし、AB=Eだけで済むのであれば、BA=Eは余分な条件ということになるのだが、この点についてはただいま研究中。だが、ちょっと証明を見た感じでは、どうも利用しているように見える....（卵が先か、鶏が先か？という問題のように見えてきた...）目がまわってきた...

練習問題として、2次正方行列の場合で、正則でない行列Aに対し、AB=Eとなる行列Bを見つけられるかどうか試しに計算してみよう。det(A)=0の例として、上で使ったA（式４）を採用しよう。Bの成分は次のようにおき、Aによってどのように表現できるか計算する。

AB=Eを計算すると、

を得る。結果が０になる式（非対角成分）にまず着目すると、a=0 or q+s=0という条件と、b=0 or p+r=0という条件が要求されることになる。次に結果が１になる式（対角成分）に着目すると、a(p+r)=1とb(q+s)=1だ。最初の２つの条件式から得られるa=0とか、b=0とかいう条件はAに科せられる条件だが、Aは与えられた行列なので自由にいじることはできない。したがって、p+r=0、およびq+s=0の方を選ぶことになるが、これは対角成分より得られた式と矛盾する。つまり、最初の２つの条件式と、最後の２つの条件式を、同時に成立させることは不可能だ。つまり、BがAの逆行列である以外にAB=Eを成立させることはできないということだ。

Aの形を一般形（式１）にして、det(A)=ad-bc=0を付帯条件に課して計算しても、同じ結論になる。